Operations Research - Definition and formulation of Assignment Problem | 12th Business Maths and Statistics : Chapter 10 : Operations Research
Chapter: 12th business maths and statistics : chapter 10 : operations research, definition and formulation of assignment problem.
Definition and formulation
Consider the problem of assigning n jobs to n machines (one job to one machine). Let C ij be the cost of assigning i th job to the j th machine and x ij represents the assignment of i th job to the j th machine.
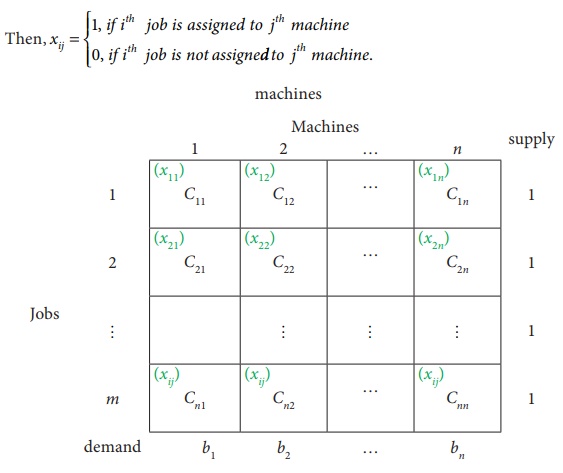
x ij is missing in any cell means that no assignment is made between the pair of job and machine.( i.e ) x ij = 0.
x ij presents in any cell means that an assignment is made their.In such cases x ij = 1
The assignment model can be written in LPP as follows
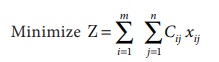
Subject to the constrains
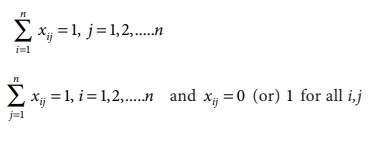
The optimum assignment schedule remains unaltered if we add or subtract a constant from all the elements of the row or column of the assignment cost matrix.
If for an assignment problem all C ij > 0 then an assignment schedule (x ij ) which satisfies ∑ C ij x ij = 0 must be optimal.
Related Topics
Privacy Policy , Terms and Conditions , DMCA Policy and Compliant
Copyright © 2018-2023 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

www.springer.com The European Mathematical Society
- StatProb Collection
- Recent changes
- Current events
- Random page
- Project talk
- Request account
- What links here
- Related changes
- Special pages
- Printable version
- Permanent link
- Page information
- View source

Assignment problem
The problem of optimally assigning $ m $ individuals to $ m $ jobs. It can be formulated as a linear programming problem that is a special case of the transport problem :
maximize $ \sum _ {i,j } c _ {ij } x _ {ij } $
$$ \sum _ { j } x _ {ij } = a _ {i} , i = 1 \dots m $$
(origins or supply),
$$ \sum _ { i } x _ {ij } = b _ {j} , j = 1 \dots n $$
(destinations or demand), where $ x _ {ij } \geq 0 $ and $ \sum a _ {i} = \sum b _ {j} $, which is called the balance condition. The assignment problem arises when $ m = n $ and all $ a _ {i} $ and $ b _ {j} $ are $ 1 $.
If all $ a _ {i} $ and $ b _ {j} $ in the transposed problem are integers, then there is an optimal solution for which all $ x _ {ij } $ are integers (Dantzig's theorem on integral solutions of the transport problem).
In the assignment problem, for such a solution $ x _ {ij } $ is either zero or one; $ x _ {ij } = 1 $ means that person $ i $ is assigned to job $ j $; the weight $ c _ {ij } $ is the utility of person $ i $ assigned to job $ j $.
The special structure of the transport problem and the assignment problem makes it possible to use algorithms that are more efficient than the simplex method . Some of these use the Hungarian method (see, e.g., [a5] , [a1] , Chapt. 7), which is based on the König–Egervary theorem (see König theorem ), the method of potentials (see [a1] , [a2] ), the out-of-kilter algorithm (see, e.g., [a3] ) or the transportation simplex method.
In turn, the transportation problem is a special case of the network optimization problem.
A totally different assignment problem is the pole assignment problem in control theory.
| [a1] | D.B. Yudin, E.G. Gol'shtein, "Linear programming" , Israel Program Sci. Transl. (1965) (In Russian) |
| [a2] | R. Frisch, "La résolution des problèmes de programme linéaire par la méthode du potentiel logarithmique" , (1956) pp. 20–23 |
| [a3] | K. Murtz, "Linear and combinatorial programming" , Wiley (1976) |
| [a4] | M. Grötschel, L. Lovász, A. Schrijver, "Geometric algorithms and combinatorial optimization" , Springer (1987) |
| [a5] | C.H. Papadimitriou, K. Steiglitz, "Combinatorial optimization" , Prentice-Hall (1982) |
- This page was last edited on 5 April 2020, at 18:48.
- Privacy policy
- About Encyclopedia of Mathematics
- Disclaimers
- Impressum-Legal
Assignment Problem: Meaning, Methods and Variations | Operations Research
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.
Meaning of Assignment Problem:
An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.
The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.
Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.
Definition of Assignment Problem:
ADVERTISEMENTS:
Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.
The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:
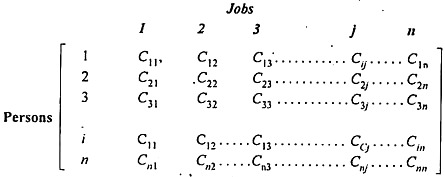
Assignment problem
1 formulation of the problem, 2 variants of the problem, 3 algorithms for solving the problem, 4 references.
Suppose that there are [math]n[/math] agents and [math]m[/math] tasks, which can be distributed between these agents. Only one task can be assigned to each agent, and each task can be assigned to only one agent. The cost of assignment of the [math]i[/math] -th task to the [math]j[/math] -th agent is [math]c(i, j)[/math] . If [math]c(i, j) = \infty[/math] , then the [math]i[/math] -th task cannot be assigned to the [math]j[/math] -th agent.
The assignment problem : find a feasible set of assignments [math]A = \{ (i_1, j_1), \ldots, (i_k, j_k) \}[/math] , [math]k = \min \{m, n\}[/math] having the maximum total cost:
If [math]m = n[/math] , then we say of the linear assignment problem : each agent is assigned to perform exactly one task, and each task is assigned to exactly one agent.
In the case of unit weights, we have to find a maximum matching in a bipartite graph, and the problem reduces to assigning as much tasks as possible.
- The Hungarian Method [1] [2] [3] for the linear problem. The complexity is [math]O(n^4)[/math] (and can be reduced [4] to [math]O(n^3)[/math] );
- the auction algorithm [5] [6] ;
- the Hopcroft-Karp algorithm [7] for the problem with unit weights. The complexity is [math]O(m \sqrt{n})[/math] .
- ↑ Kuhn, H W. “The Hungarian Method for the Assignment Problem.” Naval Research Logistics Quarterly 2, no. 1 (March 1955): 83–97. doi:10.1002/nav.3800020109.
- ↑ Kuhn, H W. “Variants of the Hungarian Method for Assignment Problems.” Naval Research Logistics Quarterly 3, no. 4 (December 1956): 253–58. doi:10.1002/nav.3800030404.
- ↑ Munkres, James. “Algorithms for the Assignment and Transportation Problems.” Journal of the Society for Industrial and Applied Mathematics 5, no. 1 (March 1957): 32–38. doi:10.1137/0105003.
- ↑ Tomizawa, N. “On Some Techniques Useful for Solution of Transportation Network Problems.” Networks 1, no. 2 (1971): 173–94. doi:10.1002/net.3230010206.
- ↑ Bertsekas, Dimitri P. “Auction Algorithms for Network Flow Problems: a Tutorial Introduction.” Computational Optimization and Applications 1 (1992): 7–66.
- ↑ Zavlanos, Michael M, Leonid Spesivtsev, and George J Pappas. “A Distributed Auction Algorithm for the Assignment Problem,” Proceedings of IEEE CDC'08, 1212–17, IEEE, 2008. doi:10.1109/CDC.2008.4739098.
- ↑ Hopcroft, John E, and Richard M Karp. “An $N^{5/2} $ Algorithm for Maximum Matchings in Bipartite Graphs.” SIAM Journal on Computing 2, no. 4 (1973): 225–31. doi:10.1137/0202019.
- Problem level
- Articles in progress
Navigation menu
Personal tools.
- Create account
- View source
- View history
- Recent changes
File storage
- Upload file
- What links here
- Related changes
- Special pages
- Printable version
- Permanent link
- Page information
- This page was last edited on 6 March 2018, at 17:08.
- Content is available under Creative Commons Attribution unless otherwise noted.
- Privacy policy
- About Algowiki
- Disclaimers
Please enable JavaScript to pass antispam protection! Here are the instructions how to enable JavaScript in your web browser http://www.enable-javascript.com . Antispam by CleanTalk.
OPERATIONS RESEARCH
Lesson 8. introduction and mathematical formulation.
Current course
Your Article Library
Assignment problem in linear programming : introduction and assignment model.
ADVERTISEMENTS:
Assignment problem is a special type of linear programming problem which deals with the allocation of the various resources to the various activities on one to one basis. It does it in such a way that the cost or time involved in the process is minimum and profit or sale is maximum. Though there problems can be solved by simplex method or by transportation method but assignment model gives a simpler approach for these problems.
In a factory, a supervisor may have six workers available and six jobs to fire. He will have to take decision regarding which job should be given to which worker. Problem forms one to one basis. This is an assignment problem.
1. Assignment Model :
Suppose there are n facilitates and n jobs it is clear that in this case, there will be n assignments. Each facility or say worker can perform each job, one at a time. But there should be certain procedure by which assignment should be made so that the profit is maximized or the cost or time is minimized.
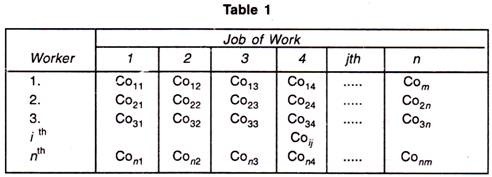
In the table, Co ij is defined as the cost when j th job is assigned to i th worker. It maybe noted here that this is a special case of transportation problem when the number of rows is equal to number of columns.
Mathematical Formulation:
Any basic feasible solution of an Assignment problem consists (2n – 1) variables of which the (n – 1) variables are zero, n is number of jobs or number of facilities. Due to this high degeneracy, if we solve the problem by usual transportation method, it will be a complex and time consuming work. Thus a separate technique is derived for it. Before going to the absolute method it is very important to formulate the problem.
Suppose x jj is a variable which is defined as
1 if the i th job is assigned to j th machine or facility
0 if the i th job is not assigned to j th machine or facility.
Now as the problem forms one to one basis or one job is to be assigned to one facility or machine.

The total assignment cost will be given by
The above definition can be developed into mathematical model as follows:
Determine x ij > 0 (i, j = 1,2, 3…n) in order to
Subjected to constraints

and x ij is either zero or one.
Method to solve Problem (Hungarian Technique):
Consider the objective function of minimization type. Following steps are involved in solving this Assignment problem,
1. Locate the smallest cost element in each row of the given cost table starting with the first row. Now, this smallest element is subtracted form each element of that row. So, we will be getting at least one zero in each row of this new table.
2. Having constructed the table (as by step-1) take the columns of the table. Starting from first column locate the smallest cost element in each column. Now subtract this smallest element from each element of that column. Having performed the step 1 and step 2, we will be getting at least one zero in each column in the reduced cost table.
3. Now, the assignments are made for the reduced table in following manner.
(i) Rows are examined successively, until the row with exactly single (one) zero is found. Assignment is made to this single zero by putting square □ around it and in the corresponding column, all other zeros are crossed out (x) because these will not be used to make any other assignment in this column. Step is conducted for each row.
(ii) Step 3 (i) in now performed on the columns as follow:- columns are examined successively till a column with exactly one zero is found. Now , assignment is made to this single zero by putting the square around it and at the same time, all other zeros in the corresponding rows are crossed out (x) step is conducted for each column.
(iii) Step 3, (i) and 3 (ii) are repeated till all the zeros are either marked or crossed out. Now, if the number of marked zeros or the assignments made are equal to number of rows or columns, optimum solution has been achieved. There will be exactly single assignment in each or columns without any assignment. In this case, we will go to step 4.
4. At this stage, draw the minimum number of lines (horizontal and vertical) necessary to cover all zeros in the matrix obtained in step 3, Following procedure is adopted:
(iii) Now tick mark all the rows that are not already marked and that have assignment in the marked columns.
(iv) All the steps i.e. (4(i), 4(ii), 4(iii) are repeated until no more rows or columns can be marked.
(v) Now draw straight lines which pass through all the un marked rows and marked columns. It can also be noticed that in an n x n matrix, always less than ‘n’ lines will cover all the zeros if there is no solution among them.
5. In step 4, if the number of lines drawn are equal to n or the number of rows, then it is the optimum solution if not, then go to step 6.
6. Select the smallest element among all the uncovered elements. Now, this element is subtracted from all the uncovered elements and added to the element which lies at the intersection of two lines. This is the matrix for fresh assignments.
7. Repeat the procedure from step (3) until the number of assignments becomes equal to the number of rows or number of columns.
Related Articles:
- Two Phase Methods of Problem Solving in Linear Programming: First and Second Phase
- Linear Programming: Applications, Definitions and Problems
No comments yet.
Leave a reply click here to cancel reply..
You must be logged in to post a comment.
Quadratic assignment problem
Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)
- 1 Introduction
- 2.1 Koopmans-Beckman Mathematical Formulation
- 2.2.1 Parameters
- 2.3.1 Optimization Problem
- 2.4 Computational Complexity
- 2.5 Algorithmic Discussions
- 2.6 Branch and Bound Procedures
- 2.7 Linearizations
- 3.1 QAP with 3 Facilities
- 4.1 Inter-plant Transportation Problem
- 4.2 The Backboard Wiring Problem
- 4.3 Hospital Layout
- 4.4 Exam Scheduling System
- 5 Conclusion
- 6 References
Introduction
The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 [1] , is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, inter-plant transportation, hospital transportation, exam scheduling, along with many other applications not described within this page.
Theory, Methodology, and/or Algorithmic Discussions
Koopmans-beckman mathematical formulation.
Economists Koopmans and Beckman began their investigation of the QAP to ascertain the optimal method of locating important economic resources in a given area. The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org.
Quadratic Assignment Problem Formulation

Inner Product

Note: The true objective cost function only requires summing entries above the diagonal in the matrix comprised of elements

Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.
Optimization Problem
With all of this information, the QAP can be summarized as:

Computational Complexity
QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who states that of all combinatorial optimization problems, QAP is the “hardest of the hard”. [2]
Algorithmic Discussions
While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:
- Dynamic Program
- Cutting Plane
Branch and Bound Procedures
The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.
The Branch and Bound method was first proposed by Ailsa Land and Alison Doig in 1960 and is the most commonly used tool for solving NP-hard optimization problems.
A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before one lists all of the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and the branch is eliminated if it cannot produce a better solution than the best one found so far by the algorithm.
Linearizations
The first attempts to solve the QAP eliminated the quadratic term in the objective function of

in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be applied. The very large number of new variables and constraints, however, usually poses an obstacle for efficiently solving the resulting linear integer programs. MILP formulations provide LP relaxations of the problem which can be used to compute lower bounds.
Numerical Example
Qap with 3 facilities.

| Permutation | Cost |
| (123) | 91.4 |
| 99.8 | |
| 98.4 | |
| 86.5 | |
| 103.3 | |
| 90 |

Applications
Inter-plant transportation problem.
The QAP was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations. [1] Factoring in the location of each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.
The Backboard Wiring Problem
As the QAP is focused on minimizing the cost of traveling from one location to another, it is an ideal approach to determining the placement of components in many modern electronics. Leon Steinberg proposed a QAP solution to optimize the layout of elements on a blackboard by minimizing the total amount of wiring required. [4]
When defining the problem Steinberg states that we have a set of n elements

as well as a set of r points

In his paper he derives the below formula:

In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation, he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.
The initial placement of components is shown below:

After the initial placement of elements, it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.
Hospital Layout
Building new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem". [5] With the high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create an optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Outpatient ward was acting as a bottleneck in the hospital and focused his efforts on optimizing the 17 departments there.
Elshafei identified the following QAP to determine where clinics should be placed:

For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 based on the original hospital layout.
Exam Scheduling System
The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross-program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.” [6]

- ↑ 1.0 1.1 1.2 Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
- ↑ 2.0 2.1 Quadratic Assignment Problem. (2020). Retrieved December 14, 2020, from https://neos-guide.org/content/quadratic-assignment-problem
- ↑ 3.0 3.1 3.2 Burkard, R. E., Çela, E., Pardalos, P. M., & Pitsoulis, L. S. (2013). The Quadratic Assignment Problem. https://www.opt.math.tugraz.at/~cela/papers/qap_bericht.pdf .
- ↑ 4.0 4.1 Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review . 1961;3(1):37.
- ↑ 5.0 5.1 Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977) . 1977;28(1):167. doi:10.2307/300878
- ↑ 6.0 6.1 Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.
Navigation menu
Quantitative Techniques: Theory and Problems by P. C. Tulsian, Vishal Pandey
Get full access to Quantitative Techniques: Theory and Problems and 60K+ other titles, with a free 10-day trial of O'Reilly.
There are also live events, courses curated by job role, and more.
WHAT IS ASSIGNMENT PROBLEM
Assignment Problem is a special type of linear programming problem where the objective is to minimise the cost or time of completing a number of jobs by a number of persons.
The assignment problem in the general form can be stated as follows:
“Given n facilities, n jobs and the effectiveness of each facility for each job, the problem is to assign each facility to one and only one job in such a way that the measure of effectiveness is optimised (Maximised or Minimised).”
Several problems of management has a structure identical with the assignment problem.
Example I A manager has four persons (i.e. facilities) available for four separate jobs (i.e. jobs) and the cost of assigning (i.e. effectiveness) each job to each ...
Get Quantitative Techniques: Theory and Problems now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
Don’t leave empty-handed
Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.
It’s yours, free.

Check it out now on O’Reilly
Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

Assignment Model | Linear Programming Problem (LPP) | Introduction
What is assignment model.
→ Assignment model is a special application of Linear Programming Problem (LPP) , in which the main objective is to assign the work or task to a group of individuals such that;
i) There is only one assignment.
ii) All the assignments should be done in such a way that the overall cost is minimized (or profit is maximized, incase of maximization).
→ In assignment problem, the cost of performing each task by each individual is known. → It is desired to find out the best assignments, such that overall cost of assigning the work is minimized.
For example:
Suppose there are 'n' tasks, which are required to be performed using 'n' resources.
The cost of performing each task by each resource is also known (shown in cells of matrix)

- In the above asignment problem, we have to provide assignments such that there is one to one assignments and the overall cost is minimized.
How Assignment Problem is related to LPP? OR Write mathematical formulation of Assignment Model.
→ Assignment Model is a special application of Linear Programming (LP).
→ The mathematical formulation for Assignment Model is given below:
→ Let, C i j \text {C}_{ij} C ij denotes the cost of resources 'i' to the task 'j' ; such that

→ Now assignment problems are of the Minimization type. So, our objective function is to minimize the overall cost.
→ Subjected to constraint;
(i) For all j t h j^{th} j t h task, only one i t h i^{th} i t h resource is possible:
(ii) For all i t h i^{th} i t h resource, there is only one j t h j^{th} j t h task possible;
(iii) x i j x_{ij} x ij is '0' or '1'.
Types of Assignment Problem:
(i) balanced assignment problem.
- It consist of a suqare matrix (n x n).
- Number of rows = Number of columns
(ii) Unbalanced Assignment Problem
- It consist of a Non-square matrix.
- Number of rows ≠ \not= = Number of columns
Methods to solve Assignment Model:
(i) integer programming method:.
In assignment problem, either allocation is done to the cell or not.
So this can be formulated using 0 or 1 integer.
While using this method, we will have n x n decision varables, and n+n equalities.
So even for 4 x 4 matrix problem, it will have 16 decision variables and 8 equalities.
So this method becomes very lengthy and difficult to solve.
(ii) Transportation Methods:
As assignment problem is a special case of transportation problem, it can also be solved using transportation methods.
In transportation methods ( NWCM , LCM & VAM), the total number of allocations will be (m+n-1) and the solution is known as non-degenerated. (For eg: for 3 x 3 matrix, there will be 3+3-1 = 5 allocations)
But, here in assignment problems, the matrix is a square matrix (m=n).
So total allocations should be (n+n-1), i.e. for 3 x 3 matrix, it should be (3+3-1) = 5
But, we know that in 3 x 3 assignment problem, maximum possible possible assignments are 3 only.
So, if are we will use transportation methods, then the solution will be degenerated as it does not satisfy the condition of (m+n-1) allocations.
So, the method becomes lengthy and time consuming.

(iii) Enumeration Method:
It is a simple trail and error type method.
Consider a 3 x 3 assignment problem. Here the assignments are done randomly and the total cost is found out.
For 3 x 3 matrix, the total possible trails are 3! So total 3! = 3 x 2 x 1 = 6 trails are possible.
The assignments which gives minimum cost is selected as optimal solution.
But, such trail and error becomes very difficult and lengthy.
If there are more number of rows and columns, ( For eg: For 6 x 6 matrix, there will be 6! trails. So 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720 trails possible) then such methods can't be applied for solving assignments problems.
(iv) Hungarian Method:
It was developed by two mathematicians of Hungary. So, it is known as Hungarian Method.
It is also know as Reduced matrix method or Flood's technique.
There are two main conditions for applying Hungarian Method:
(1) Square Matrix (n x n). (2) Problem should be of minimization type.
Suggested Notes:
Modified Distribution Method (MODI) | Transportation Problem | Transportation Model
Stepping Stone | Transportation Problem | Transportation Model
Vogel’s Approximation Method (VAM) | Method to Solve Transportation Problem | Transportation Model

Transportation Model - Introduction
North West Corner Method | Method to Solve Transportation Problem | Transportation Model
Least Cost Method | Method to Solve Transportation Problem | Transportation Model
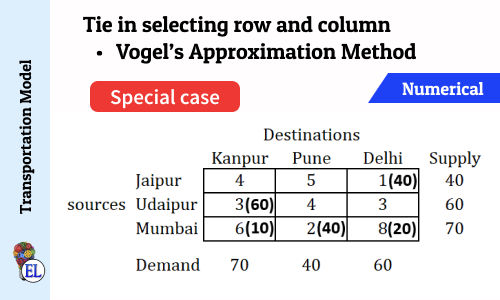
Tie in selecting row and column (Vogel's Approximation Method - VAM) | Numerical | Solving Transportation Problem | Transportation Model

Crashing Special Case - Multiple (Parallel) Critical Paths

Crashing Special Case - Indirect cost less than Crash Cost

Basics of Program Evaluation and Review Technique (PERT)

Numerical on PERT (Program Evaluation and Review Technique)

Network Analysis - Dealing with Network Construction Basics

Construct a project network with predecessor relationship | Operation Research | Numerical
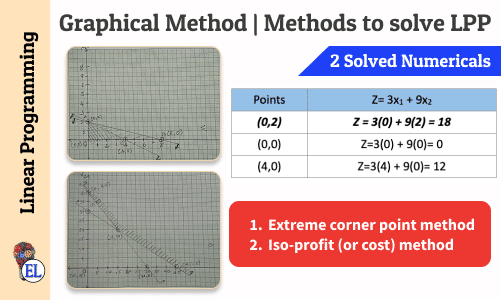
Graphical Method | Methods to solve LPP | Linear Programming
Basics of Linear Programming

Linear Programming Problem (LPP) Formulation with Numericals

All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct .
Want to tell us something privately? Contact Us
Post comment

Education Lessons
Stay in touch, [notes] operation research, [notes] dynamics of machinery, [notes] maths, [notes] science, [notes] computer aided design.

Assignment Problem
- Feb 20, 2024
The assignment problem is a special case of transportation problem.
Suppose there are $n$ jobs to be performed and $n$ persons are available for these jobs. Assume that each person can do each job at a time, though with varying degree of efficiency.
Let $c_{ij}$ be the cost if the $i^{th}$ person is assigned the $j^{th}$ job. Then the problem is to find an assignment so that the total cost of performing all jobs is minimum. (i.e., which job should be assigned to which person with minimum cost). Such problem is called an Assignment Problem (AP).
The tabular form of the assignment problem is as follows
| Persons \ Jobs | $1$ | $2$ | $\cdots$ | $j$ | $\cdots$ | $n$ |
|---|---|---|---|---|---|---|
| Persons/ Jobs | $1$ | $2$ | $\cdots$ | $j$ | $\cdots$ | $n$ |
| $1$ | $c_{11}$ | $c_{12}$ | $\cdots$ | $c_{1j}$ | $\cdots$ | $c_{1n}$ |
| $2$ | $c_{21}$ | $c_{22}$ | $\cdots$ | $c_{2j}$ | $\cdots$ | $c_{2n}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| $i$ | $c_{i1}$ | $c_{i2}$ | $\cdots$ | $c_{ij}$ | $\cdots$ | $c_{in}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| $n$ | $c_{n1}$ | $c_{n2}$ | $\cdots$ | $c_{nj}$ | $\cdots$ | $c_{nn}$ |
The above table is called the $n\times n$ cost-matrix, where $c_{ij}$ are real numbers.
Thus the objective in the Assignment Problem is to assign a number of jobs to the equal number of persons at a minimum cost or maximum profit. e.g. assigning men to offices, classes to rooms, drivers to trucks, problems to research teams etc.
Mathematical Formulation of AP
Mathematically, the AP can be stated as $$ \begin{equation}\label{eq2.4} \min z = \sum_{i=1}^n\sum_{j=1}^n x_{ij} c_{ij}. \end{equation} $$ subject to $$ \begin{equation}\label{eq2.5} \sum_{j=1}^n x_{ij} =1,; \text{ for } i=1,2,\ldots, n \end{equation} $$
$$ \begin{equation}\label{eq2.6} \sum_{i=1}^n x_{ij} =1,; \text{ for } j=1,2,\ldots,n \end{equation} $$ where $$ \begin{equation*} x_{ij}=\left{ \begin{array}{ll} 1, & \hbox{if $i^{th}$ person is assigned $j^{th}$ job;} \ 0, & \hbox{otherwise.} \end{array} \right. \end{equation*} $$ Constraint \eqref{eq2.5} indicate that one job is done by $i^{th}$ person $i=1,2,\ldots, n$ and constraint \eqref{eq2.6} indicate that one person should be assigned $j^{th}$ job $j=1,2,\ldots, n$.
It may be observed from the above formulation that AP is a special type of Linear programming problem.
Unbalanced Assignment Problem
If the cost matrix of an assignment problem is not a square matrix, the assignment problem is called an Unbalanced Assignment Problem . In such a case, add dummy row or dummy column with zero cost in the cost matrix so as to form a square matrix. Then apply the usual assignment method to find the optimal solution.
Maximal Assignment Problem
Sometimes, the assignment problem deals with the maximization of an objective function instead of minimization.. For example, it may be required to assign persons to jobs in such a way that the expected profit is maximum. In such a case, first convert the problem of maximization to minimization and apply the usual procedure of assignment.
The assignment problem of maximization type can be converted to minimization type by subtracting all the elements of the given profit matrix from the largest element.
Restrictions on Assignment
Sometimes due to technical or other difficulties do not permit the assignment of a particular facility to a particular job. In such a situation, the difficulty can be overcome by assigning a very high cost (say, infinity i.e. $\infty$) to the corresponding cell.
Because of assigning an infinite penalty to such a cell the activity will be automatically excluded from the optimal solution. Then apply the usual procedure to find the optimal assignment.

LIVE Course for free
- Ask a Question

Give the mathematical form of the assignment problem.
- operations research
Please log in or register to add a comment.
The mathematical form of assignment problem is Minimize Z = \(∑^n_{i = 1}∑^n_{j = 1} C_{ij}x_{ij}\)
Subject to the constraints
(or) 1 for all i = 1, 2, …….. n and j = 1, 2, …….. n
where C ij is the cost of assigning ith job to jth machine and x ij represents the assignment of ith job to jth machine.
Find MCQs & Mock Test
- JEE Main 2025 Test Series
- NEET Test Series
- Class 12 Chapterwise MCQ Test
- Class 11 Chapterwise Practice Test
- Class 10 Chapterwise MCQ Test
- Class 9 Chapterwise MCQ Test
- Class 8 Chapterwise MCQ Test
- Class 7 Chapterwise MCQ Test
Related questions
Welcome to Sarthaks eConnect: A unique platform where students can interact with teachers/experts/students to get solutions to their queries. Students (upto class 10+2) preparing for All Government Exams, CBSE Board Exam , ICSE Board Exam , State Board Exam, JEE (Mains+Advance) and NEET can ask questions from any subject and get quick answers by subject teachers/ experts/mentors/students.
- All categories
- JEE (36.6k)
- NEET (9.2k)
- Science (780k)
- Mathematics (254k)
- Statistics (3.0k)
- Environmental Science (5.4k)
- Biotechnology (703)
- Social Science (126k)
- Commerce (74.9k)
- Electronics (3.9k)
- Computer (21.7k)
- Artificial Intelligence (AI) (3.3k)
- Information Technology (20.2k)
- Programming (13.1k)
- Political Science (10.2k)
- Home Science (8.1k)
- Psychology (4.4k)
- Sociology (7.1k)
- English (66.9k)
- Hindi (29.8k)
- Aptitude (23.7k)
- Reasoning (14.8k)
- Olympiad (535)
- Skill Tips (91)
- RBSE (49.1k)
- General (72.9k)
- MSBSHSE (1.8k)
- Mathematics (1.5k)
- Physics (1.9k)
- Chemistry (4.3k)
- Bio Botany (1.3k)
- Bio Zoology (1.4k)
- English (867)
- Commerce (1.0k)
- Economics (1.5k)
- Accountancy (812)
- Computer Science (1.2k)
- Computer Applications (1.7k)
- Applications of Matrices and Determinants (89)
- Integral Calculus I (146)
- Integral Calculus II (94)
- Differential Equations (104)
- Numerical Methods (61)
- Random Variable and Mathematical Expectation (88)
- Probability Distributions (104)
- Sampling Techniques and Statistical Inference (81)
- Applied Statistics (126)
- Operations Research (72)
- Class 11 (18.6k)
- Class 10 (6.1k)
- Class 9 (3.7k)
- Class 8 (4.4k)
- Class 7 (4.2k)
- Class 6 (3.8k)
- Kerala Board (24.5k)
- Send feedback
- Privacy Policy
- Terms of Use
- Refund Policy
- Analysis of Algorithms
- Backtracking
- Dynamic Programming
- Divide and Conquer
- Geometric Algorithms
- Mathematical Algorithms
- Pattern Searching
- Bitwise Algorithms
- Branch & Bound
- Randomized Algorithms
Quadratic Assignment Problem (QAP)
- Channel Assignment Problem
- Assignment Operators In C++
- Solidity - Assignment Operators
- Job Assignment Problem using Branch And Bound
- Worker-Bike Assignments (Campus Bikes)
- Range Minimum Query with Range Assignment
- Transportation Problem | Set 1 (Introduction)
- Transportation Problem | Set 2 (NorthWest Corner Method)
- Transportation Problem | Set 3 (Least Cost Cell Method)
- Transportation Problem | Set 4 (Vogel's Approximation Method)
- Minimum boats to save people
- Assignment Operators in C
- QA - Placement Quizzes | Profit and Loss | Question 7
- QA - Placement Quizzes | Profit and Loss | Question 4
- QA - Placement Quizzes | Profit and Loss | Question 12
- QA - Placement Quizzes | Profit and Loss | Question 10
- QA - Placement Quizzes | Age | Question 4
- IBM Placement Paper | Quantitative Analysis Set - 5
- IBM Placement Paper | Quantitative Analysis Set - 4
The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them.
The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows.
The distance matrix and flow matrix, as well as restrictions to ensure each facility is assigned to exactly one location and each location is assigned to exactly one facility, can be used to formulate the QAP as a quadratic objective function.
The QAP is a well-known example of an NP-hard problem , which means that for larger cases, computing the best solution might be difficult. As a result, many algorithms and heuristics have been created to quickly identify approximations of answers.
There are various types of algorithms for different problem structures, such as:
- Precise algorithms
- Approximation algorithms
- Metaheuristics like genetic algorithms and simulated annealing
- Specialized algorithms
Example: Given four facilities (F1, F2, F3, F4) and four locations (L1, L2, L3, L4). We have a cost matrix that represents the pairwise distances or costs between facilities. Additionally, we have a flow matrix that represents the interaction or flow between locations. Find the assignment that minimizes the total cost based on the interactions between facilities and locations. Each facility must be assigned to exactly one location, and each location can only accommodate one facility.
Facilities cost matrix:
| L1 | L2 | L3 | L4 | |
|---|---|---|---|---|
| F1 | 0 | 2 | 3 | 1 |
| F2 | 2 | 0 | 1 | 4 |
| F3 | 3 | 1 | 0 | 2 |
| F4 | 1 | 4 | 2 | 0 |
Flow matrix:
| F1 | F2 | F3 | F4 | |
|---|---|---|---|---|
| L1 | 0 | 1 | 2 | 3 |
| L2 | 1 | 0 | 4 | 2 |
| L3 | 2 | 4 | 0 | 1 |
| L4 | 3 | 2 | 1 | 0 |
To solve the QAP, various optimization techniques can be used, such as mathematical programming, heuristics, or metaheuristics. These techniques aim to explore the search space and find the optimal or near-optimal solution.
The solution to the QAP will provide an assignment of facilities to locations that minimizes the overall cost.
The solution generates all possible permutations of the assignment and calculates the total cost for each assignment. The optimal assignment is the one that results in the minimum total cost.
To calculate the total cost, we look at each pair of facilities in (i, j) and their respective locations (location1, location2). We then multiply the cost of assigning facility1 to facility2 (facilities[facility1][facility2]) with the flow from location1 to location2 (locations[location1][location2]). This process is done for all pairs of facilities in the assignment, and the costs are summed up.
Overall, the output tells us that assigning facilities to locations as F1->L1, F3->L2, F2->L3, and F4->L4 results in the minimum total cost of 44. This means that Facility 1 is assigned to Location 1, Facility 3 is assigned to Location 2, Facility 2 is assigned to Location 3, and Facility 4 is assigned to Location 4, yielding the lowest cost based on the given cost and flow matrices.This example demonstrates the process of finding the optimal assignment by considering the costs and flows associated with each facility and location. The objective is to find the assignment that minimizes the total cost, taking into account the interactions between facilities and locations.
Applications of the QAP include facility location, logistics, scheduling, and network architecture, all of which require effective resource allocation and arrangement.
Please Login to comment...
Similar reads, improve your coding skills with practice.
What kind of Experience do you want to share?
Information
- Author Services
Initiatives
You are accessing a machine-readable page. In order to be human-readable, please install an RSS reader.
All articles published by MDPI are made immediately available worldwide under an open access license. No special permission is required to reuse all or part of the article published by MDPI, including figures and tables. For articles published under an open access Creative Common CC BY license, any part of the article may be reused without permission provided that the original article is clearly cited. For more information, please refer to https://www.mdpi.com/openaccess .
Feature papers represent the most advanced research with significant potential for high impact in the field. A Feature Paper should be a substantial original Article that involves several techniques or approaches, provides an outlook for future research directions and describes possible research applications.
Feature papers are submitted upon individual invitation or recommendation by the scientific editors and must receive positive feedback from the reviewers.
Editor’s Choice articles are based on recommendations by the scientific editors of MDPI journals from around the world. Editors select a small number of articles recently published in the journal that they believe will be particularly interesting to readers, or important in the respective research area. The aim is to provide a snapshot of some of the most exciting work published in the various research areas of the journal.
Original Submission Date Received: .
- Active Journals
- Find a Journal
- Proceedings Series
- For Authors
- For Reviewers
- For Editors
- For Librarians
- For Publishers
- For Societies
- For Conference Organizers
- Open Access Policy
- Institutional Open Access Program
- Special Issues Guidelines
- Editorial Process
- Research and Publication Ethics
- Article Processing Charges
- Testimonials
- Preprints.org
- SciProfiles
- Encyclopedia

Article Menu
- Subscribe SciFeed
- Recommended Articles
- Google Scholar
- on Google Scholar
- Table of Contents
Find support for a specific problem in the support section of our website.
Please let us know what you think of our products and services.
Visit our dedicated information section to learn more about MDPI.
JSmol Viewer
Solving optimal electric vehicle charger deployment problem.

1. Introduction
- Building a comprehensive mathematical framework accommodating the particular complexity,
- Demonstrating our numerical computational framework for solving the facility location problem (FLP) representing the optimal location;
- Laying out an extensive comparative study among the optimization solving techniques as an effort to find the most efficient solver;
- Applying the findings to two real-world case studies representing an average and high density of EVs.
2. Related Work
2.1. problem formulation approaches, 2.1.1. facility location problem (flp), 2.1.2. distance optimization, 2.1.3. weight assignment techniques, 2.1.4. machine learning techniques, 2.2. solving techniques, 3. problem formulation, 3.1. spatial setup, 3.2. formulation to capacitated flp.
- i and j are indexes for an EV charging facility and a demanding area (or, equivalently, a customer), respectively.
- v i j gives the variable cost to obtain the electricity supplied to serve customer j .
- d j gauges the demand from customer j .
- y i j quantifies the fraction of the demand made by customer j and fulfilled by facility i .
- x i indicates whether facility i opens or not .
- s i denotes the sunken cost (also known as “fixed” cost) of opening a charging facility i .
- E i , j defines the equity achieved at customer j via service from facility i .
- C i and C min indicate the capacity of facility i and the required minimum capacity of any facility, respectively, both in the unit of kWh.
3.3. Unique Challenges
- C1: Large search spaces for domain and other variables;
- C2: Inexistence of polynomial-time numerical solving. techniques
4. Solving Techniques Development
4.1. unique challenges and proposed approaches, 4.2. comparison among solving techniques, 4.3. alternative techniques, 5. case study 1: region with average ev density, 5.1. case-specific refinement of solving method, 5.2. results and discussion.
| SA implemented in this work |
| temperature neighbor |
6. Case Study 2: Region with High EV Density
6.1. case-specific refinement of solving method, 6.1.1. data collection and preprocessing, 6.1.2. data integration, 6.1.3. training methods.
- Data Preparation: The collected and merged dataset undergoes preprocessing to ensure its suitability for training, including handling missing values, data normalization, and feature engineering.
- Model Selection: The decision tree (DT) [ 67 ], support vector machine (SVM) [ 68 ], and random forest (RF) [ 69 ] models are considered as potential candidates for training due to their widespread usage in site selection problems.
- Training Process: Each selected model is trained using the prepared dataset, which is divided into training and validation sets. Performance evaluation metrics such as accuracy, precision, recall, and F1 score are utilized to assess the model’s performance during training.
- Model Evaluation: After training, the models are evaluated using the validation set to assess their predictive capabilities. The evaluation metrics are used to compare the models’ performance and identify the model with the highest accuracy or other desired performance metrics.
- Model Selection: Based on the evaluation results, the model demonstrating the best performance is selected as the final machine learning model for the site selection task.
6.2. Results and Discussions
- Installation criteria differ between DC fast chargers and level-2 chargers. Significant differences in consistency are observed when training separately based on each charging station type or when training with both types together. Consequently, it can be concluded that chargers have been installed at locations that meet their respective criteria for both DC fast chargers and level-2 chargers.
- Non-uniform distribution of reference data does not significantly affect training results. There is no significant difference in consistency between training based on non-uniformly distributed chargers and training based on grid points uniformly distributed at regular intervals. Thus, it can be concluded that the non-uniform distribution of data does not impact the training results.
- Buffer size influences data consistency. Decreasing the buffer size results in increased consistency. The reason for the decrease in consistency at buffer sizes below 125 m is that the polygon data used for learning is 250 m × 250 m grid data, resulting in buffers that do not contain data from the 125 m radius buffer size. This problem can be solved by using smaller grid data than 250 m × 250 m grid data during data preprocessing. In conclusion, this result shows that larger buffer sizes increase data redundancy and affect consistency.
7. Conclusions and Future Work
Author contributions, institutional review board statement, informed consent statement, data availability statement, acknowledgments, conflicts of interest.
- Gersdorf, T.; Hensley, R.; Hertzke, P.; Schaufuss, P.; Tschiesner, A. The Road Ahead for E-Mobility ; McKinsey: Chicago, IL, USA, 2020. [ Google Scholar ]
- The White House. Fact sheet: The Biden-Harris electric vehicle charging action plan. In Statements and Releases ; The White House: Washington, DC, USA, 2021. [ Google Scholar ]
- United States Department of Transportation. Biden-Harris Administration Announces $ 1.5 Billion Available through the 2023 RAISE Grant Program ; United States Department of Transportation: Washington, DC, USA, 2022.
- Mitchell, R. U.S. government will pay Tesla to open its charger network to non-Tesla EVs. Los Angeles Times , 15 February 2023. [ Google Scholar ]
- Newburger, E. All 50 States Get Green Light to Build EV Charging Stations Covering 75,000 Miles of Highways ; CNBC: Englewood Cliffs, NJ, USA, 2022. [ Google Scholar ]
- LNG2019. The Average Distance between Gas Stations in the United States. November 2022. Available online: https://www.linkedin.com/pulse/how-many-gas-stations-united-states-timothy-ohagan/ (accessed on 1 May 2024).
- Bauer, G.; Hsu, C.; Lutsey, N. When Might Lower-Income Drivers Benefit from Electric Vehicles? Quantifying the Economic Equity Implications of Electric Vehicle Adoption ; ICCT Working Paper; International Council on Clean Transportation: Washington, DC, USA, 2021. [ Google Scholar ]
- Moghaddam, V.; Ahmad, I.; Habibi, D.; Masoum, M. Dispatch management of portable charging stations in electric vehicle networks. ETransportation 2021 , 8 , 100112. [ Google Scholar ] [ CrossRef ]
- Onat, N.; Kucukvar, M.; Aboushaqrah, N.; Jabbar, R. How sustainable is electric mobility? A comprehensive sustainability assessment approach for the case of Qatar. Appl. Energy 2019 , 250 , 461–477. [ Google Scholar ] [ CrossRef ]
- Qiao, B.; Liu, J. Multi-objective dynamic economic emission dispatch based on electric vehicles and wind power integrated system using differential evolution algorithm. Renew. Energy 2020 , 154 , 316–336. [ Google Scholar ] [ CrossRef ]
- Jakob, K.; Pruzan, P. The simple plant location problem: Survey and synthesis. Eur. J. Oper. Res. 1983 , 12 , 41. [ Google Scholar ]
- Ayazi, S.; Askarzadeh, A. Finding optimal path of feeder routing problem in power distribution network by an efficient and new methodology. Int. Trans. Elect. Energy Syst. 2021 , 31 , e13196. [ Google Scholar ] [ CrossRef ]
- Floudas, C.; Lin, X. Mixed integer linear programming in process scheduling: Modeling, algorithms, and applications. Ann. Operat. Res. 2005 , 139 , 131–162. [ Google Scholar ] [ CrossRef ]
- Shen, X.; Shahidehpour, M.; Zhu, S.; Han, Y.; Zheng, J. Multi-stage planning of active distribution networks considering the co-optimization of operation strategies. IEEE Trans. Smart Grid 2016 , 9 , 1425–1433. [ Google Scholar ] [ CrossRef ]
- Kim, K.; Goo, Y. Optimizing fast EV charging infrastructure location with traffic flow data. Innov. Stud. 2020 , 15 , 61–91. [ Google Scholar ] [ CrossRef ]
- Kim, J.; Lee, D.; Kim, S. A study to determine the optimized location for fast electric vehicle charging station considering charging demand in seoul. J. Korea Inst. Intell. Transp. Syst. 2022 , 21 . [ Google Scholar ] [ CrossRef ]
- Yun, C. The case study of priority installation area of electric vehicle charging infrastructure using bigdata standard reference analysis model. Proc. Symp. Korean Inst. Commun. Inform. Sci. 2019 , 23–26. [ Google Scholar ]
- Jo, J.; Kim, S. A Study on the optimal location selection for hydrogen refueling stations on a highway using machine learning. J. Cadastre Land InformatiX 2021 , 51 , 83–106. [ Google Scholar ]
- Hernandez, A.; Perez, M.; Gupta, S.; Muntes-Mulero, V. Using machine learning to optimize parallelism in big data applications. Future Gener. Comput. Syst. 2018 , 86 , 1076–1092. [ Google Scholar ] [ CrossRef ]
- Klotz, E.; Newman, A. Practical guidelines for solving difficult mixed integer linear programs. Surv. Operat. Res. Manag. Sci. 2013 , 18 , 18–32. [ Google Scholar ] [ CrossRef ]
- Abdel-Basset, M.; Manogaran, G.; Rashad, H.; Zaied, A. A comprehensive review of quadratic assignment problem: Variants, hybrids and applications. J. Ambient Intell. Human Comput. 2018 . [ Google Scholar ] [ CrossRef ]
- Zhang, H.; Beltran-Royo, C.; Ma, L. Solving the quadratic assignment problem by means of general purpose mixed integer linear programming solvers. Ann. Operat. Res. 2013 , 207 , 261–278. [ Google Scholar ] [ CrossRef ]
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. 2003 , 35 , 268–308. [ Google Scholar ] [ CrossRef ]
- Bianchi, L.; Dorigo, M.; Gambardella, L.; Gutjahr, W. A survey on metaheuristics for stochastic combinatorial optimization. Nat. Comput. 2008 , 8 , 239–287. [ Google Scholar ] [ CrossRef ]
- Drezner, Z. The extended concentric tabu for the quadratic assignment problem. Eur. J. Operat. Res. 2005 , 160 , 416–422. [ Google Scholar ] [ CrossRef ]
- Misevicius, A. An implementation of the iterated tabu search algorithm for the quadratic assignment problem. Operat. Res. Spectrum 2012 , 34 , 665–690. [ Google Scholar ] [ CrossRef ]
- Drezner, Z. Compounded genetic algorithms for the quadratic assignment problem. Operat. Res. Lett. 2005 , 33 , 475–480. [ Google Scholar ] [ CrossRef ]
- Misevicius, A. An improved hybrid optimization algorithm for the quadratic assignment problem. Math. Model. Anal. 2004 , 9 , 149–168. [ Google Scholar ] [ CrossRef ]
- Talbi, E.; Roux, O.; Fonlupt, C.; Robillard, D. Parallel ant colonies for the quadratic assignment problem. Future Gener. Comput. Syst. 2001 , 17 , 441–449. [ Google Scholar ] [ CrossRef ]
- Benlic, U.; Hao, J. Memetic search for the quadratic assignment problem. Expert Syst. Appl. 2015 , 42 , 584–595. [ Google Scholar ] [ CrossRef ]
- Gini, C. Variability and mutability. J. Roy. Statist. Soc. 1913 , 76 , 476–477. [ Google Scholar ]
- Dai, L.; Jia, Y.; Liang, L.; Chang, Z. Metric and control of system fairness in heterogeneous networks. In Proceedings of the 2017 23rd Asia-Pacific Conference on Communications (APCC), Perth, Australia, 11–13 December 2017. [ Google Scholar ]
- Williams, D. Feds Approve Georgia DOT Plan for EV Charging Stations ; Georgia Public Broadcasting: Atlanta, GA, USA, 2022. [ Google Scholar ]
- Nicholas, M. Estimating Electric Vehicle Charging Infrastructure Costs across Major US Metropolitan Areas ; Working Paper 2019-14; ICCT: Washington, DC, USA, 2019. [ Google Scholar ]
- Kleinert, T.; Labbe, M.; Ljubic, I.; Schmidt, M. A survey on mixed-integer programming techniques in bilevel optimization. EURO J. Comput. Optim. 2021 , 9 , 100007. [ Google Scholar ] [ CrossRef ]
- Deng, X.; Lv, T. Power system planning with increasing variable renewable energy: A review of optimization models. J. Clean. Prod. 2020 , 246 , 118962. [ Google Scholar ] [ CrossRef ]
- Schenker, C.; Cohen, J.; Acar, E. A flexible optimization framework for regularized matrix-tensor factorizations with linear couplings. IEEE J. Sel. Topics Signal Process. 2020 , 15 , 506–521. [ Google Scholar ] [ CrossRef ]
- Burkard, R.; Fortuna, T.; Hurkens, C. Makespan minimization for chemical batch processes using non-uniform time grids. Comput. Chem. Eng. 2002 , 26 , 1321–1332. [ Google Scholar ] [ CrossRef ]
- Asghari, M.; Fathollahi-Fard, A.; Al-e-hashem, S.M.; Dulebenets, M. Transformation and linearization techniques in optimization: A state-of-the-art survey. Mathematics 2022 , 10 , 283. [ Google Scholar ] [ CrossRef ]
- Hardman, S.; Fleming, K.; Khare, E.; Ramadan, M. A perspective on equity in the transition to electric vehicle. MIT Sci. Policy Rev. 2021 , 2 , 46–54. [ Google Scholar ] [ CrossRef ]
- Mandi, J.; Stuckey, P.; Guns, T. Smart predict-and-optimize for hard combinatorial optimization problems. Proc. AAAI Conf. Artificial Intell. 2020 , 34 , 1603–1610. [ Google Scholar ] [ CrossRef ]
- Baluja, S.; Davies, S. Using Optimal Dependency-Trees for Combinatorial Optimization: Learning the Structure of the Search Space ; Carnegie-Mellon University: Pittsburgh, PA, USA, 1997. [ Google Scholar ]
- Hyde, K.; Maier, H.; Colby, C. A distance-based uncertainty analysis approach to multi-criteria decision analysis for water resource decision making. J. Environ. Manag. 2005 , 77 , 278–290. [ Google Scholar ] [ CrossRef ]
- Estalaki, W.M.; Kerachian, R.; Nikoo, M. Developing water quality management policies for the Chitgar urban lake: Application of fuzzy social choice and evidential reasoning methods. Environ. Earth Sci. 2016 , 75 , 1–16. [ Google Scholar ] [ CrossRef ]
- Madani, K.; Read, L.; Shalikarian, L. Voting under uncertainty: A stochastic framework for analyzing group decision-making problems. Water Resour. Manag. 2014 , 28 , 1839–1856. [ Google Scholar ] [ CrossRef ]
- Fowler, R.; Paterson, M.; Tanimoto, S. Optimal packing and covering in the plane are NP-complete. Inform. Proc. Lett. 1981 , 12 , 133–137. [ Google Scholar ] [ CrossRef ]
- Megiddo, N.; Tamir, A. On the complexity of locating linear facilities in the plane. Operat. Res. Lett. 1993 , 1 , 194–197. [ Google Scholar ] [ CrossRef ]
- Kirkpatrick, S.; Gelatt, C., Jr.; Vecchi, M. Optimization by simulated annealing. Science 1983 , 220 , 671–680. [ Google Scholar ] [ CrossRef ]
- Clausen, J.; Perregaard, M. Solving large quadratic assignment problems in parallel. Comput. Opt. Appl. 1997 , 8 , 111–127. [ Google Scholar ] [ CrossRef ]
- Luong, T.; Melab, N.; Talbi, E. GPU computing for parallel local search metaheuristic algorithms. IEEE Trans. Comput. 2011 , 62 , 173–185. [ Google Scholar ] [ CrossRef ]
- Sonuc, E.; Sen, B.; Bayir, S. A cooperative GPU-based parallel multistart simulated annealing algorithm for quadratic assignment problem. Eng. Sci. Technol., Int. J. 2018 , 21 , 843–849. [ Google Scholar ] [ CrossRef ]
- Website of NVIDIA’s CUDA Zone. Available online: https://developer.nvidia.com/cuda-zone (accessed on 10 October 2023).
- Zhu, W.; Curry, J.; Marquez, A. SIMD tabu search for the quadratic assignment problem with graphics hardware acceleration. Int. J. Prod. Res. 2010 , 48 , 1035–1047. [ Google Scholar ] [ CrossRef ]
- Abdelkafi, O.; Derbel, B.; Liefooghe, A. A parallel tabu search for the large-scale quadratic assignment problem. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019. [ Google Scholar ]
- Ghosh, D.; Goldengorin, B.; Sierksma, G. Data correcting algorithms in combinatorial optimization. In Handbook Combinatorial Optimization ; Springer: Boston, MA, USA, 2004; Volume 5, pp. 1–53. [ Google Scholar ]
- Dantzig, G. Linear Programming and Extensions , 6th ed.; Princeton University Press: Princeton, NJ, USA, 1974; pp. 545–547. [ Google Scholar ]
- Rastrigin, L. Systems of Extremal Control ; Nauka: Moscow, Russia, 1974. [ Google Scholar ]
- Katoch, S.; Chauhan, S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools App. 2021 , 80 , 8091–8126. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Dupanloup, I.; Schneider, S.; Excoffier, L. A simulated annealing approach to define the genetic structure of populations. Mol. Ecol. 2002 , 11 , 2571–2581. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987 , 2 , 37–52. [ Google Scholar ] [ CrossRef ]
- Website of MATLAB Parallel Server. Available online: https://www.mathworks.com/products/matlab-parallel-server.html (accessed on 1 February 2023).
- Website of Georgia State Government. Available online: https://www.georgia.org/mobility-infrastructure#/analyze?show_map=true®ion=US-GA (accessed on 12 May 2023).
- Power Planning Department Demand Forecast Team. Electric Vehicle and Charger Supply and Use Analysis ; Korea Power Exchange: Naju-si, Republic of Korea, 2021. [ Google Scholar ]
- Kang, C.; Jeon, S. A Study on Establishment of Proper Installation Criteria of Electric Vehicle Charging Station in Gyeonggi-Do ; Gyeonggi Research Institute: Suwon, Republic of Korea, 2017. [ Google Scholar ]
- Website of QGIS 3.36. Available online: https://www.qgis.org/en/site/ (accessed on 12 October 2023).
- Jeon, H.; Park, J.; Kim, H. A Study on the optimum location selection of electric vehicle fast charging station using GIS. KSCE 2022 Conv. 2022 , 558–562. [ Google Scholar ]
- Charbuty, B.; Abdulazeez, A. Classification based on decision tree algorithm for machine learning. J. Appl. Sci. Technol. Trends 2021 , 2 , 20–28. [ Google Scholar ] [ CrossRef ]
- Hearst, M.; Dumais, S.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their App. 1998 , 13 , 18–28. [ Google Scholar ] [ CrossRef ]
- Breiman, L. Random forests. Mach. Learn. 2001 , 5–32. [ Google Scholar ] [ CrossRef ]
Click here to enlarge figure
| Literature | Contribution |
|---|---|
| FLP | Formulation into MINLP for various real-world problems |
| Distance Optimization | Stochastic analyses for location selection |
| Weight Assignment Techniques | Demand prediction by assigning weights to data |
| Machine Learning Techniques | More efficient weight assignment via priority prediction |
| Solving Techniques | Exact or heuristic approaches to solve NP-hard problems |
| This Paper | Comprehensive feasibility study encompassing the aforementioned numerical techniques |
| Solver | ⋯ | Objective Value | Number of Iterations | |||
|---|---|---|---|---|---|---|
| Integer Linear Programming | ⋯ | 0 | 0 | |||
| Pattern Search | 0 | 0 | ⋯ | 0 | 0 | 204 |
| Genetic Algorithm | −0.062657 | 0.042974 | ⋯ | −0.041941 | 1.4801 | 3907 |
| Particle Swarm | ⋯ | 4320 | ||||
| Simulated Annealing | −1.99 | ⋯ | 0.00018799 | 3.9798 | 3008 | |
| Surrogate Optimization | 0.99678 | 1.9937 | ⋯ | 1.9832 | 8.9671 | 200 |
| Model Name | Decision Tree | Support Vector Machine | Random Forest |
|---|---|---|---|
| Consistency | 0.6583 | 0.4295 | 0.7580 |
| Precision | 0.6712 | 0.1845 | 0.7580 |
| Recall | 0.6583 | 0.4295 | 0.7580 |
| F1-Score | 0.6593 | 0.2581 | 0.7509 |
| Setting Condition | Buffer Size | Consistency | |
|---|---|---|---|
| Baseline | Public DC fast chargers and random point | 1.13 km | 0.7580 |
| a. Charging Station Type | Public level-2 chargers and random point | 1.13 km | 0.7678 |
| Public DC fast chargers and public level-2 chargers and random point | 1.13 km | 0.6284 | |
| b. Uniform Distribution of Reference Data | Center point of grid data | 1.13 km | 0.7649 |
| c. Buffer size | Public DC fast chargers and random point | 700 m | 0.8176 |
| 600 m | 0.8355 | ||
| 500 m | 0.8611 | ||
| 400 m | 0.8743 | ||
| 300 m | 0.9003 | ||
| 200 m | 0.9182 | ||
| 150 m | 0.9348 | ||
| 125 m | 0.9395 | ||
| 100 m | 0.9293 | ||
| 50 m | 0.8969 |
| Data | Variable Importance [%] |
|---|---|
| POI | 16.9264 |
| Surface | 12.9745 |
| Building0 | 11.3435 |
| Work_Population | 9.4463 |
| Building3 | 8.1137 |
| Traffic | 7.3983 |
| Building1 | 6.768 |
| Flow_Population | 5.7931 |
| Car | 5.4492 |
| EV_Car | 5.3769 |
| Parking | 4.2025 |
| Tour | 3.563 |
| Building2 | 2.6447 |
| The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
Share and Cite
Kim, S.; Jeong, Y.; Nam, J.-W. Solving Optimal Electric Vehicle Charger Deployment Problem. Appl. Sci. 2024 , 14 , 5092. https://doi.org/10.3390/app14125092
Kim S, Jeong Y, Nam J-W. Solving Optimal Electric Vehicle Charger Deployment Problem. Applied Sciences . 2024; 14(12):5092. https://doi.org/10.3390/app14125092
Kim, Seungmo, Yeonho Jeong, and Jae-Won Nam. 2024. "Solving Optimal Electric Vehicle Charger Deployment Problem" Applied Sciences 14, no. 12: 5092. https://doi.org/10.3390/app14125092
Article Metrics
Article access statistics, further information, mdpi initiatives, follow mdpi.

Subscribe to receive issue release notifications and newsletters from MDPI journals

IMAGES
VIDEO
COMMENTS
Definition and formulation. Consider the problem of assigning n jobs to n machines (one job to one machine). Let Cij be the cost of assigning ith job to the jth machine and xij represents the assignment of ith job to the jth machine. xij is missing in any cell means that no assignment is made between the pair of job and machine. (i.e) xij = 0.
The assignment problem consists of finding, in a weighted bipartite graph, a matching of a given size, in which the sum of weights of the edges is minimum. If the numbers of agents and tasks are equal, then the problem is called balanced assignment. Otherwise, it is called unbalanced assignment. [1] If the total cost of the assignment for all ...
The assignment problem arises when $ m = n $ and all $ a _ {i} $ and $ b _ {j} $ are $ 1 $. If all $ a _ {i} $ and $ b _ {j} $ in the transposed problem are integers, then there is an optimal solution for which all $ x _ {ij } $ are integers (Dantzig's theorem on integral solutions of the transport problem).
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations. Meaning of Assignment Problem: An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total ...
8.1 Introduction. An assignment problem is a particular case of transportation problem in which a number of operations are to be assigned to an equal number of operators, where each operator performs only one operation. The objective is to minimize overall cost or to maximize the overall profit for a given assignment schedule.
The assignment problem is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics. In an assignment problem , we must find a maximum matching that has the minimum weight in a weighted bipartite graph .
This lecture discusses the assignment problemsOther videos @DrHarishGarg Assignment Problem - Mathematical Models: Link: https://youtu.be/OX1ssZez_sYHungaria...
Formulation of Assignment ProblemAn assignment problem is a special form of transportation problem where all supply and demand values equal one. A distinguis...
The Hungarian Method: The following algorithm applies the above theorem to a given n × n cost matrix to find an optimal assignment. Step 1. Subtract the smallest entry in each row from all the entries of its row. Step 2. Subtract the smallest entry in each column from all the entries of its column. Step 3.
1 Formulation of the problem. Suppose that there are [math]n[/math] agents and [math]m[/math] tasks, which can be distributed between these agents. Only one task can be assigned to each agent, and each task can be assigned to only one agent. The cost of assignment of the [math]i[/math]-th task to the [math]j[/math]-th agent is [math]c(i, j)[/math].If [math]c(i, j) = \infty[/math], then the ...
the objective is to maximise the effectiveness through Assignment, Hungarian Method can be applied to a revised cost matrix obtained from the original matrix. Balanced Assignment Problem: Balanced Assignment Problem is an assignment problem where the number of facilities is equal to the number of jobs. Unbalanced Assignment Problem:
8.3 Mathematical Formulation of Assignment Problem . Using the notations described above, the assignment problem consist of finding the values of X ij in order to minimize the total cost Subject to restrictions where X ij denotes the j th job to be assigned to the i th person. An assignment problem could thus be solved by Simplex Method.
Mathematical Formulation: Any basic feasible solution of an Assignment problem consists (2n - 1) variables of which the (n - 1) variables are zero, n is number of jobs or number of facilities. Due to this high degeneracy, if we solve the problem by usual transportation method, it will be a complex and time consuming work. Thus a separate ...
Koopmans-Beckman Mathematical Formulation. ... Quadratic Assignment Problem Formulation Parameters = () is an n x n matrix ... Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.
Assignment Problem is a special type of linear programming problem where the objective is to minimise the cost or time of completing a number of jobs by a number of persons. The assignment problem in the general form can be stated as follows: "Given n facilities, n jobs and the effectiveness of each facility for each job, the problem is to ...
Linear programming (LP) can be defined as' a mathematical method of determining an optimum assignment of interdependent activities, given the availability of resources'. LP models may be constructed for ... 2.2 Formulation of Assignment Problem[34] The decision problem becomes complicated when a number of resources are required to be ...
How Assignment Problem is related to LPP? OR Write mathematical formulation of Assignment Model. → Assignment Model is a special application of Linear Programming (LP). → The mathematical formulation for Assignment Model is given below: → Let, C i j \text {C}_{ij} C ij denotes the cost of resources 'i' to the task 'j'; such that
Unbalanced Assignment Problem. If the cost matrix of an assignment problem is not a square matrix, the assignment problem is called an Unbalanced Assignment Problem. In such a case, add dummy row or dummy column with zero cost in the cost matrix so as to form a square matrix. Then apply the usual assignment method to find the optimal solution.
A mathematical formulation of the problem. Let x and y represent the number of cabinets of kind 1 and 2 that he must produce. Non-negative constraints are non-negative limitations. The company is allowed to invest 540 hours of labour and must build up to 50 cabinets. Hence, 15x + 9y <= 540. x + y <= 50.
9. Do the same for some variants of assignment problems. 10. Give the name of an algorithm that can solve huge assignment problems that are well beyond the scope of Solver. Transportation problems were introduced in Section 3.5 and Section 3.6 did the same for assignment problems.
history of sophisticated mathematical techniques, many of which built on linear programming for generating a global view of large, complex optimization problems [5]. 2. Mathemtical LP Model for assignment problem Some linear programming models for the assignment problem is presented .It is assumed that the cost (or time) for every
An optimal solution of an assignment problem can be obtained only if, _____ (a) each row and column has only one zero element asked Aug 27, 2020 in Operations Research by Vijay01 ( 48.1k points) operations research
The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them. The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows. The distance ...
Electric vehicles (EVs) have already been acknowledged to be the most viable solution to the climate change that the entire globe has long been combating. Along the same line, it is a salient subject to expand the availability of EV charging infrastructure, which quintessentially necessitates the optimization of the charger's locations. This paper proposes to formulate the optimal EV charger ...