

Geometric Sequences – Examples and Practice Problems
Geometric sequences have the main characteristic of having a common ratio, which is multiplied by the last term to find the next term. Any term in a geometric sequence can be found using a formula.
Here, we will look at a summary of geometric sequences and we will explore its formula. In addition, we will see several examples with answers and exercises to solve to practice these concepts.
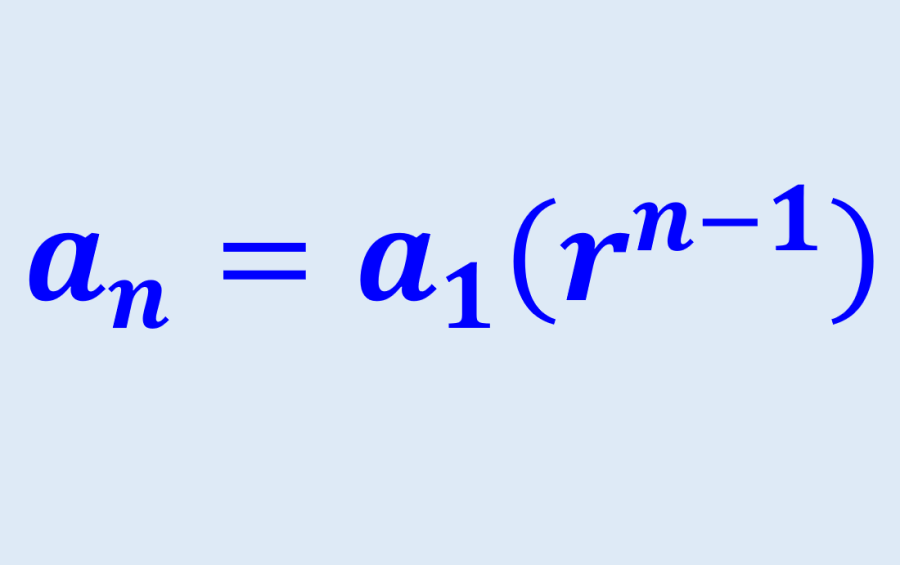
Relevant for …
Exploring examples with answers of geometric sequences.
See examples
Summary of geometric sequences
Geometric sequences – examples with answers, geometric sequences – practice problems.
Geometric sequences are sequences in which the next number in the sequence is found by multiplying the previous term by a number called the common ratio . The common ratio is denoted by the letter r .
Depending on the common ratio, the geometric sequence can be increasing or decreasing. If the common ratio is greater than 1, the sequence is increasing and if the common ratio is between 0 and 1, the sequence is decreasing:

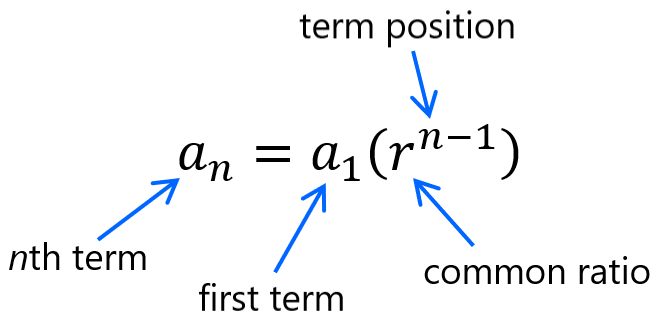
We can find any number in the geometric sequence using the geometric sequence formula:
We can find the common ratio by dividing any term by the previous term:
$latex r=\frac{a_{n}}{a_{n-1}}$
Find the next term in the geometric sequence: 4, 8, 16, 32, ? .
First, we have to find the common ratio of the geometric progression. To do this, we divide a term by the previous term:
- $latex \frac{32}{16}=2$
- $latex \frac{16}{8}=2$
- $latex \frac{8}{4}=2$
Therefore, the common ratio is 2. To find the next term, we multiply the last term by the common ratio: $latex 32\times 2=64$.
What is the next term in the geometric sequence? 3, 15, 75, 375, ? .
We start by finding the common ratio for the geometric progression. Then, we divide each term by its previous term:
- $latex \frac{375}{75}=5$
- $latex \frac{75}{15}=5$
- $latex \frac{15}{3}=5$
We see that the common ratio is 5. We find the next term by multiplying the last term by the common ratio : $latex 375 \times 5=1875$.
Determine the next term in the geometric sequence: 48, 24, 12, 6, ? .
Again, we start by finding the common ratio in the progression:
- $latex \frac{6}{12}=0.5$
- $latex \frac{12}{24}=0.5$
- $latex \frac{24}{48}=0.5$
In this case, we see that the common ratio is between 0 and 1, so the progression is slowing down. The next term in the geometric progression is $latex 6\times 0.5=3$.
What is the value of the 6th term of a geometric sequence where the first term is 3 and the common ratio is 2?
We have the following values:
- First term: $latex a_{1}=3$
- Common ratio: $latex r=2$
- Position of term: $latex n=6$
Then, we can use the formula for geometric sequences with the given values:
$latex a_{n}=a_{1}(r^{n-1})$
$latex a_{6}=3(2^{6-1})$
$latex a_{6}=3(2^{5})$
$latex a_{6}=5(32)$
$latex a_{6}=160$
Find the 12th term in the geometric sequence: 5, 15, 45, 135, …
In this case, we have to use the formula of geometric progressions $latex a_{n}=a_{1}({{r}^{n-1}})$. Therefore, we have to identify the first term, the common reason and the position of the term:
- First term: $latex a_{1}=5$
- Common ratio: $latex r=3$
- Position of term: $latex n=12$
Now, we substitute this data into the formula:
$latex a_{n}=a_{1}({{r}^{n-1}})$
$latex a_{12}=5({{3}^{12-1}})$
$latex a_{12}=5({{3}^{11}})$
$latex a_{12}=5(177147)$
$latex a_{12}=885 735$
We see that we have a very large number. Geometric progressions tend to grow rapidly depending on the common proportion.
Find the 8th term in the geometric sequence 8, 32, 128, 512, …
Again, we start by identifying the first term, the common ratio, and the position of the term to be used with the formula:
- First term: $latex a_{1}=8$
- Common ratio: $latex r=4$
- Position of term: $latex n=8$
Now, we use the formula with these values:
$latex a_{8}=8({{4}^{8-1}})$
$latex a_{8}=8({{4}^{7}})$
$latex a_{8}=8(16384)$
$latex a_{8}=131072$
Find the 10th term in the geometric sequence: 168, 84, 42, 21, …
In this case, we have a decreasing geometric progression, so we expect the common ratio to be between 0 and 1:
- First term: $latex a_{1}=168$
- Common ratio: $latex r=0.5$
- Position of term: $latex n=10$
We use the formula to find the term 10:
$latex a_{10}=168({{0.5}^{10-1}})$
$latex a_{10}=168({{0.5}^{9}})$
$latex a_{10}=168(0.001953)$
$latex a_{10}=0.328$
Find the 7th term in the geometric sequence: 540, 180, 60, 20, …
Similar to the previous example, here we have a decreasing geometric progression, so the common ratio must be between 0 and 1:
- First term: $latex a_{1}=540$
- Common ratio: $latex r=\frac{1}{3}$
- Possiion of term: $latex n=7$
We use these values to substitute in the formula:
$latex a_{7}=540({{\left( \frac{1}{3}\right)}^{7-1}})$
$latex a_{7}=540({{\left( \frac{1}{3}\right)}^{6}})$
$latex a_{7}=540(0.0013717)$
$latex a_{7}=0.7407$
If the 4th term of a geometric sequence is 16 and the 7th term is 128, what is the 11th term?
In this case, we know neither the value of the first term nor the common ratio. However, we can start by forming the following equations:
$latex a_{4}=a_{1}(r^{4-1})$
$latex 16=a_{1}(r^{3})~~~[1]$
$latex a_{7}=a_{1}(r^{7-1})$
$latex 128=a_{1}(r^{6})~~~[2]$
If we divide equation 2 by equation 1, we have:
$$\frac{128}{16}=\frac{a_{1}(r^{6})}{a_{1}(r^{3})$$
$latex 8=r^{3}$
$latex r=2$
If we consider the 7th term as the 1st term, the 11th term is now the 5th term:
- First term: $latex a_{1}=128$
- Position of term: $latex n=5$
Using these values in the formula, we have:
$latex a_{5}=128(2^{5-1})$
$latex a_{5}=128(2^4)$
$latex a_{5}=128(16)$
$latex a_{5}=2048$
Then, the 11th term of the given sequence is 2048.
A geometric sequence has a 3rd term equal to 256 and an 8th term equal to -8. What is the value of the 14th term?
Similar to the previous example, we can find the common ratio by forming the following equations:
$latex a_{3}=a_{1}(r^{3-1})$
$latex 256=a_{1}(r^{2})~~~[1]$
$latex a_{8}=a_{1}(r^{8-1})$
$latex -8=a_{1}(r^{7})~~~[2]$
Now we divide them to obtain:
$$\frac{-8}{256}=\frac{a_{1}(r^{7})}{a_{1}(r^{2})$$
$$-\frac{1}{32}=r^{5}$$
$$r=-\frac{1}{2}$$
Considering the 8th term as the first term, the 14th term corresponds to the 7th term. Then:
- First term: $latex a_{1}=-8$
- Common ratio: $latex r=-\frac{1}{2}$
- Position of term: $latex n=7$
Using the formula, we have:
$$a_{7}=-8(-\frac{1}{2}^{7-1})$$
$$a_{7}=-8(-\frac{1}{2}^6)$$
$$a_{7}=-8(\frac{1}{64})$$
$$a_{7}=-\frac{1}{8}$$
Then, the 14th term of the given sequence is $latex -\frac{1}{8}$.

In a geometric sequence, the 4th term is 135 and 7th term is 3645. What is the value of the 15th term?
Write the answer in the input box.
Interested in learning more about sequences? Take a look at these pages:
- Arithmetic and Geometric Sequences
- Examples of Arithmetic Sequences

Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.

Learn mathematics with our additional resources in different topics

Copyright © 2024 Neurochispas
All rights reserved.
INFORMATION
Terms and Conditions
Privacy Policy
About Neurochispas
About the Author

Free Mathematics Tutorials
- Math Problems
- Algebra Questions and Problems
- Graphs of Functions, Equations, and Algebra
- Free Math Worksheets to Download
- Analytical Tutorials
- Solving Equation and Inequalities
- Online Math Calculators and Solvers
- Free Graph Paper
- Math Software
- The Applications of Mathematics in Physics and Engineering
- Exercises de Mathematiques Utilisant les Applets
- Calculus Tutorials and Problems
- Calculus Questions With Answers
- Free Calculus Worksheets to Download
- Geometry Tutorials and Problems
- Online Geometry Calculators and Solvers
- Free Geometry Worksheets to Download
- Trigonometry Tutorials and Problems for Self Tests
- Free Trigonometry Questions with Answers
- Free Trigonometry Worksheets to Download
- Elementary Statistics and Probability Tutorials and Problems
- Mathematics pages in French
- About the author
- Primary Math
- Middle School Math
- High School Math
- Free Practice for SAT, ACT and Compass Math tests
Geometric Sequences Problems with Solutions
Geometric sequences are used in several branches of applied mathematics to engineering, sciences, computer sciences, biology, finance... Problems and exercises involving geometric sequences, along with answers are presented.
Review OF Geometric Sequences
The sequence shown below
Problems with Solutions
Problem 1 Find the terms a 2 , a 3 , a 4 and a 5 of a geometric sequence if a 1 = 10 and the common ratio r = - 1. Solution to Problem 1: Use the definition of a geometric sequence \( a_2 = a_1 \times r = 10 (-1) = - 10 \\ a_3 = a_2 \times r = - 10 (-1) = 10 \\ a_4 = a_3 \times r = 10 (-1) = - 10 \\ a_5 = a_4 \times r = - 10 (-1) = 10 \)
Find the 10 th term of a geometric sequence if a 1 = 45 and the common ration r = 0.2. Solution to Problem 2: Use the formula \[ a_n = a_1 \times r^{n-1} \] that gives the n th term to find a 10 as follows \( a_{10} = 45 \times 0.2^{10-1} = 2.304 \times 10^{-5} \)
Find a 20 of a geometric sequence if the first few terms of the sequence are given by
Given the terms a 10 = 3 / 512 and a 15 = 3 / 16384 of a geometric sequence, find the exact value of the term a 30 of the sequence. Solution to Problem 4: We first use the formula for the n th term to write a 10 and a 15 as follows \( a_{10} = a_1 \times r^{10-1} = a_1 r^9 = 3 / 512 \\ \\ a_{15} = a_1 \times r^{15-1} = a_1 r^{14} = 3 / 16384 \) We now divide the terms a 10 and a 15 to write \( a_{15} / a_{10} = a_1 \times r^{14} / (a_1 \times r^9) = (3 / 16384) / (3 / 512) \) Simplify expressions in the above equation to obtain. r 5 = 1 / 32 which gives r = 1/2 We now use a 10 to find a 1 as follows. \( a_{10} = 3 / 512 = a_1 (1/2)^9 \) Solve for a 1 to obtain. \( a_1 = 3 \) We now use the formula for the n th term to find a 30 as follows. \( a_{30} = 3(1/2)^{29} = 3 / 536870912 \)
Find the sum \[ S = \sum_{k=1}^{6} 3^{k - 1} \] Solution to Problem 5: We first rewrite the sum S as follows S = 1 + 3 + 9 + 27 + 81 + 243 = 364 Another method is to first note that the terms making the sum are those of a geometric sequence with a 1 = 1 and r = 3 using the formula s n = a 1 (1 - r n ) / (1 - r) with n = 6. s 6 = 1 (1 - 3 6 ) / (1 - 3) = 364
Find the sum \[ S = \sum_{i=1}^{10} 8 \times (1/4)^{i - 1} \] Solution to Problem 6: An examination of the terms included in the sum are 8 , 8× ((1/4) 1 , 8×((1/4) 2 , ... , 8×((1/4) 9 These are the terms of a geometric sequence with a 1 = 8 and r = 1/4 and therefore we can use the formula for the sum of the terms of a geometric sequence s 10 = a 1 (1 - r n ) / (1 - r) = 8 × (1 - (1/4) 10 ) / (1 - 1/4) = 10.67 (rounded to 2 decimal places)
Write the rational number 5.31313131... as the ratio of two integers. Solution to Problem 7: We first write the given rational number as an infinite sum as follows 5.313131... = 5 + 0.31 + 0.0031 + 0.000031 + .... The terms making 0.31 + 0.0031 + 0.000031 ... are those of a geometric sequence with a 1 = 0.31 and r = 0.01. Hence the use of the formula for an infinite sum of a geometric sequence S = a 1 / (1 - r) = 0.31 / (1 - 0.01) = 0.31 / 0.99 = 31 / 99 We now write 5.313131... as follows 5.313131... = 5 + 31/99 = 526 / 99
Exercises with Answers
Answer the following questions related to geometric sequences: a) Find a 20 given that a 3 = 1/2 and a 5 = 8 b) Find a 30 given that the first few terms of a geometric sequence are given by -2 , 1 , -1/2 , 1/4 ... c) Find r given that a 1 = 10 and a 20 = 10 -18 d) write the rational number 0.9717171... as a ratio of two positive integers.
a) a 20 = 2 18 b) a 30 = 1 / 2 28 c) r = 0.1 d) 0.9717171... = 481/495
More References and links
- Arithmetic Sequences Problems with Solutions
- math problems with detailed solutions
- Math Tutorials and Problems
POPULAR PAGES
- Math Problems, Questions and Online Self Tests
- Arithmetic Sequences Online Calculator
- Trigonometry Problems and Questions with Solutions - Grade 10
- Geometry Problems with Answers and Solutions - Grade 10
privacy policy
One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
This topic is relevant for:

Geometric Sequences
Here we will learn what a geometric sequence is, how to continue a geometric sequence, how to find missing terms in a geometric sequence, and how to generate a geometric sequence.
At the end, you’ll find geometric sequence worksheets based on Edexcel, AQA, and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is a geometric sequence?
A geometric sequence (geometric progression) is an ordered set of numbers that progresses by multiplying or dividing each term by a common ratio.
If we multiply or divide by the same number each time to make the sequence, it is a geometric sequence .
The common ratio is the same for any two consecutive terms in the same sequence.
Here are a few examples,
| First Term | Term-to-Term Rule | First 5 Terms |
|---|---|---|
| 3 | Multiply by 3 | 3, 9, 27, 81, 243, ... |
| 5 | Multiply by 2 | 5, 10, 20, 40, 80, ... |
| -12 | Divide by 2 | -12, -6, -3, -1.5, -0.75, ... |
| 0.8 | Multiply by 5 | 0.8, 4, 20, 100, 500, ... |
| \frac{1}{2} | Divide by 4 | \frac{1}{2}, \; \frac{1}{8}, \; \frac{1}{32}, \; \frac{1}{128}, \; \frac{1}{512} \ldots |
What are geometric sequences?

Geometric sequence formula
The geometric sequence formula is,
Where,
\pmb{ a_{n} } is the n^{th} term (general term),
\pmb{ a_{1} } is the first term,
\pmb{ n } is the term position,
and \pmb{ r } is the common ratio.
We get the geometric sequence formula by looking at the following example,

We can see the common ratio (r) is 2 , so r = 2 .
a_{1} is the first term which is 5 ,
a_{2} is the second term which is 10 ,
and a_{3} is the third term which is 20 etc.
However we can write this using the common difference of 2 ,
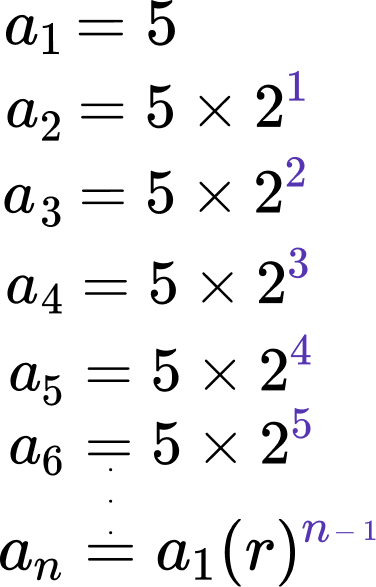
Related lessons on sequences
Geometric sequences is part of our series of lessons to support revision on sequences . You may find it helpful to start with the main sequences lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
- Quadratic sequences
- Arithmetic sequence
- Nth term of a sequence
- Recurrence relation
- Quadratic nth term
How to continue a geometric sequence
To continue a geometric sequence, you need to calculate the common ratio. This is the factor that is used to multiply one term to get the next term. To calculate the common ratio and continue a geometric sequence you need to:
Take two consecutive terms from the sequence.
- Divide the second term by the first term to find the common ratio r .
Multiply the last term in the sequence by the common ratio to find the next term. Repeat for each new term.
Explain how to continue a geometric sequence

Geometric sequences worksheet
Get your free geometric sequences worksheet of 20+ questions and answers. Includes reasoning and applied questions.
Continuing a geometric sequence examples
Example 1: continuing a geometric sequence.
Calculate the next three terms for the geometric progression 1, 2, 4, 8, 16, …
Here we will take the numbers 4 and 8 .
2 Divide the second term by the first term to find the value of the common ratio, r .
3 Multiply the last term in the sequence by the common ratio to find the next term. Repeat for each new term.
The next three terms in the sequence are 32, 64, and 128 .
Example 2: continuing a geometric sequence with negative numbers
Calculate the next three terms for the sequence -2, -10, -50, -250, -1250, …
Here we will take the numbers -10 and -50 .
Divide the second term by the first term to find the common ratio, r.
The next three terms are -6250, -31250, and -156250.
Example 3: continuing a geometric sequence with decimals
Calculate the next three terms for the sequence 100, 10, 1, 0.1, 0.01, …
Here we will take the numbers 0.1 and 0.01 .
Divide the second term by the first term to find the common ratio, r .
The next three terms in the sequence are 0.001, 0.0001, and 0.00001.
Example 4: continuing a geometric sequence involving fractions
Calculate the next three terms for the sequence
Here we will take the numbers 5 and 2\frac{1}{2} .
The next three terms are
\frac{5}{16}, \frac{5}{32}, and \frac{5}{64} .
Geometric sequence practice questions – continue the sequence
1. Write the next three terms of the sequence 0.5, 5, 50, 500, …

Choose two consecutive terms. For example, 5 and 50 .
Common ratio,
2. Write the next three terms of the sequence 0.04, 0.2, 1, 5, 25, …
Choose two consecutive terms. For example, 5 and 25 .
3. Calculate the next 3 terms of the sequence -1, -3, -9, -27, -81, …
Choose two consecutive terms. For example, -27 and -9 .
4. By finding the common ratio, state the next 3 terms of the sequence 640, 160, 40, 10, 2.5 .
Choose two consecutive terms. For example, 40 and 10 .
5. Work out the common ratio and therefore the next three terms in the sequence 36, 12, 4, \frac{4}{3}, \frac{4}{9}, …
Choose two consecutive terms. For example, 12 and 4 .
6. Find the common ratio and hence calculate the next three terms of the sequence 1, -1, 1, -1, 1, …
Choose two consecutive terms. For example, -1 and 1 .
How to find missing numbers in a geometric sequence
The common ratio can be used to find missing numbers in a geometric sequence. To find missing numbers in a geometric sequence you need to:
Calculate the common ratio between two consecutive terms.
- Multiply the term before any missing value by the common ratio.
Divide the term after any missing value by the common ratio.
Repeat Steps 2 and 3 until all missing values are calculated. You may only need to use Step 2 or 3 depending on what terms you have been given.
Explain how to find missing numbers in a geometric sequence

Finding missing numbers in a geometric sequence examples
Example 5: find the missing numbers in the geometric sequence.
Fill in the missing terms in the sequence 7, 14, …, …,112 .
Multiply the term before any missing value by the common ratio.
The missing terms are 28 and 56 .
Note: Here, you could repeat Step 2 by using 28 \times 2 = 56.
Example 6: find the missing numbers in a geometric sequence including decimals
Find the missing values in the sequence 0.4, …, ..., 137.2, 960.4.
Divide the term after any missing value by the common ratio.
The missing terms are 2.8 and 19.6 .
Example 7: find the missing numbers in a geometric sequence when there are multiple consecutive terms missing
Find the missing values in the sequence, -4, ..., …, -108,...
First, we need to find the factor between the two terms, -108 \div -4 = 27 .
To get from -108 to -4 , we jump 3 terms.
This means that -4 has been multiplied by the common ratio three times or -4 \times r \times r \times r = -4r^3 .
\begin{aligned} r^{3}&=27\\\\ r&=3 \end{aligned}
Note: Term -108 is already given.
The missing terms are -12, -36, and -324.
We don’t need to complete this step.
Example 8: find the missing numbers in a geometric sequence including mixed numbers
Find the missing values in the sequence
Calculate the common ratio between two consecutive terms.
Repeat this step to find the next term.
40 \frac{1}{2} \times 3=121 \frac{1}{2}
The missing terms in the sequence are
1 \frac{1}{2}, 40 \frac{1}{2}, and 121 \frac{1}{2} .
Geometric sequence practice questions – find missing numbers
1. Find the missing numbers in the geometric sequence 4, 2, …, 0.5, …
Choose two consecutive terms. For example, 4 and 2 .
2. Find the missing numbers in the sequence -7, -35, …, …, -4375
Choose two consecutive terms. For example, -7 and -35 .
3. Find the missing terms in the sequence 0.6, …, …, 0.075, 0.0375
Choose two consecutive terms. For example, 0.075 and 0.0375 .
4. Calculate the missing terms in the arithmetic sequence 2 \frac{1}{5}, \frac{11}{20}, \frac{11}{80}, \ldots, \ldots
Choose two consecutive terms. For example, \frac{11}{20} and \frac{11}{80} .
5. Work out the missing terms in the sequence 3, …, …, 24 .
3 has been multiplied by the common ratio, r, three times to get 24.
3 \times r \times r \times r=24 \text{ or } 3r^{3}=24 .
Solving the equation,
6. Work out the missing terms in the sequence 90, …, …, \frac{10}{3} .
90 has been multiplied by the common ratio, r, three times to get \frac{10}{3}.
90 \times r \times r \times r=\frac{10}{3} \text{ or } 90r^{3}=\frac{10}{3} .
How to generate a geometric sequence
In order to generate a geometric sequence, we need to know the n^{th} term. Using a as the first term of the sequence, r as the common ratio and n to represent the position of the term, the n^{th} term of a geometric sequence is written as ar^{n-1}.
Once we know the first term and the common ratio, we can work out any number of terms in the sequence.
The first term is found when n=1 , the second term when n=2 , the third term when n=3 and so on.
To generate a geometric sequence you need to:
- Substitute n=1 into the n^{th} term to calculate the first term.
- Substitute n=2 into the n^{th} term to calculate the second term.
Continue to substitute values for n until all the required terms of the sequence are calculated.
Explain how to generate a geometric sequence

Generating a geometric sequence examples
Example 9: generate a geometric sequence using the n th term.
Generate the first 5 terms of the sequence 4^{n-1} .
Substitute n = 1 into the n^{th} term to calculate the first term.
When n = 1,\quad 4^{1-1} = 4^{0} = 1 .
Substitute n = 2 into the n^{th} term to calculate the second term.
When n = 2,\quad 4^{2-1 }= 4^{1} = 4 .
When n=3, \quad 4^{3-1}=4^{2}=16 .
When n=4, \quad 4^{4-1}=4^{3}=64 .
When n=5, \quad 4^{5-1}=4^{4}=256 .
The first 5 terms of the sequence are 1, 4, 16, 64, 256.
Example 10: generate a geometric sequence using a table
Complete the table for the first 5 terms of the arithmetic sequence 6 \times 2^{n-1}.
| 1 | 2 | 3 | 4 | 5 | |
| 2 | |||||
| 6 × 2 |
| 1 | 2 | 3 | 4 | 5 | |
| 2 | 2 = 1 | ||||
| 6 × 2 | 6 |
| 1 | 2 | 3 | 4 | 5 | |
| 2 | 2 = 1 | 2 = 2 | |||
| 6 × 2 | 6 | 12 |
| 1 | 2 | 3 | 4 | 5 | |
| 2 | 2 = 1 | 2 = 2 | 2 = 4 | 2 = 8 | 2 = 16 |
| 6 × 2 | 6 | 12 | 24 | 48 | 96 |
Example 11: generate larger terms in a geometric sequence
A geometric sequence has the n^{th} term \left(\frac{1}{2}\right)^{n} .
Calculate the 1^{st}, 2^{nd}, 10^{th} and 12^{th} terms in the sequence. Express your answers as fractions.
When n=1,\quad \left(\frac{1}{2}\right)^{1}=\frac{1}{2} .
Substitute n = 2 into the n^{th} term to calculate the second term.
When n=2, \quad \left(\frac{1}{2}\right)^{2}=\frac{1}{4} .
When n=10,\quad \left(\frac{1}{2}\right)^{10}=\frac{1}{1024} .
When n=12,\quad \left(\frac{1}{2}\right)^{12}=\frac{1}{4096} .
The unknown terms are
1, \frac{1}{4}, \frac{1}{1024}, and \frac{1}{4096} .
Example 12: generate a geometric sequence with a negative common ratio
Generate the first 5 terms of the geometric sequence 2(- 3)^{n-1} .
When n=1, \quad 2(-3)^{n-1}=2(-3)^{1-1}=2(-3)^{0}=2 \times 1=2 .
When n=2,\quad 2(-3)^{n-1}=2(-3)^{2-1}=2(-3)^{1}=2 \times-3=-6 .
When n=3, \quad 2(-3)^{n-1}=2(-3)^{3-1}=2(-3)^{2}=2 \times 9=18 .
When n=4, \quad 2(-3)^{n-1}=2(-3)^{4-1}=2(-3)^{3}=2 \times-27=-54 .
When n=5, \quad 2(-3)^{n-1}=2(-3)^{5-1}=2(-3)^{4}=2 \times 81=162 .
The first 5 terms of the sequence are 2, -6, 18, -54, and 162 .
Geometric sequence practice questions – generate a sequence
1. Generate the first 5 terms of the sequence 10^{n} .
When n=1, 10^{1}=10 .
When n=2, 10^{2}=100 .
When n=3, 10^{3}=1000 .
When n=4, 10^{4}=10000 .
When n=5, 10^{5}=100000 .
2. Generate the first 5 terms of the sequence 5^{n-1} .
When n=1, 5^{1-1}=5^{0}=1 .
When n=2, 5^{2-1}=5^{1}=5 .
When n=3, 5^{3-1}=5^{2}=25 .
When n=4, 5^{4-1}=5^{3}=125 .
When n=5, 5^{5-1}=5^{4}=625 .
3. Generate the first 5 terms of the sequence 4 \times 3^{n-1} .
When n=1, 4 \times 3^{1-1}=4 \times 3^{0}=4 .
When n=2, 4 \times 3^{2-1}=4 \times 3^{1}=12 .
When n=3, 4 \times 3^{3-1}=4 \times 3^{2}=36 .
When n=4, 4 \times 3^{4-1}=4 \times 3^{3}=108 .
When n=5, 4 \times 3^{5-1}=4 \times 3^{4}=324 .
4. Generate the first 5 terms of the sequence \frac{3^{n}}{6} .
When n=1, \frac{3^1}{6}= \frac{1}{2} .
When n=2, \frac{3^2}{6}= \frac{9}{6} = 1 \frac{1}{2} .
When n=3, \frac{3^3}{6}= \frac{27}{6} = 4 \frac{1}{2} .
When n=4, \frac{3^4}{6}= \frac{81}{6} = 13 \frac{1}{2} .
When n=5, \frac{3^5}{6}= \frac{243}{6} = 40 \frac{1}{2} .
5. Calculate the 1st, 3rd, 10th and 15th term of the sequence 2^{n} .
When n=1, 2^{1}= 2 .
When n=3, 2^{3}= 8 .
When n=10, 2^{10}= 1024 .
When n=15, 2^{15}= 32768 .
6. Calculate the first 5 terms of the sequence 3 \times (-5)^{n-1} .
When n=1, 3 \times (-5)^{1-1} = 3 \times (-5)^{0} = 3 .
When n=2, 3 \times (-5)^{2-1} = 3 \times (-5)^{1} = -15 .
When n=3, 3 \times (-5)^{3-1} = 3 \times (-5)^{2} = 75 .
When n=4, 3 \times (-5)^{4-1} = 3 \times (-5)^{3} = -375 .
When n=5, 3 \times (-5)^{5-1} = 3 \times (-5)^{4} = 1875 .
Geometric sequences GCSE exam questions
1. Which sequence is a geometric progression?
1, 3, 5, 7, 9,…. \quad \quad \quad 1, 3, 9, 27, 81, …..
1, 3, 6, 10, 15, …. \quad \quad 1, 0.6, 0.2, -0.2, -0.6,….
1, 3, 9, 27, 81, …..
2. Here is a geometric progression,
1, -5, 25, …., 625, …
(a) Find the common ratio.
(b) Work out the fourth term of the sequence.
25 \div -5 = – 5
Common ratio = -5
25 \times -5
3. A scientist is studying a type of bacteria. The number of bacteria over the first four days is shown below.
| Day 1 | Day 2 | Day 3 | Day 4 |
| 60 | 180 | 540 | 1620 |
How many bacteria will there be on day 7?
180 \div 60 = 3
1620 \times 3 \times 3 \times 3
Common misconceptions
- Mixing up the common ratio with the common difference for arithmetic sequences
Although these two phrases are similar, each successive term in a geometric sequence of numbers is calculated by multiplying the previous term by a common ratio and not by adding a common difference.
- A negative value for r means that all terms in the sequence are negative
This is not always the case as when r is raised to an even power, the solution is always positive.
- The first term in a geometric sequence
The first term is a . With ar^{n-1} , the first term would occur when n = 1 and so the power of r would be equal to 0 . Anything to the power of 0 is equal to 1 , leaving a as the first term in the sequence. This is usually mistaken when a = 1 as it is not clearly noted in the question for example, 2^{n-1} is the same as 1 \times 2^{n-1} .
- Incorrect simplifying of the n th term
For example, 6 \times 3^{n-1} is incorrectly simplified to 18^{n-1} as 6 \times 3 = 18 .
- The difference between an arithmetic and a geometric sequence
Arithmetic sequences are formed by adding or subtracting the same number. Geometric sequences are formed by multiplying or dividing the same number.
Learning checklist
You have now learned how to:
- Recognise geometric sequences
The next lessons are
- Inequalities
- Functions in algebra
- Laws of indices
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.
Privacy Overview
Geometric Sequences and Sums
A Sequence is a set of things (usually numbers) that are in order.
Geometric Sequences
In a Geometric Sequence each term is found by multiplying the previous term by a constant .
Example: 1, 2, 4, 8, 16, 32, 64, 128, 256, ...
This sequence has a factor of 2 between each number.
Each term (except the first term) is found by multiplying the previous term by 2 .
In General we write a Geometric Sequence like this:
{a, ar, ar 2 , ar 3 , ... }
- a is the first term, and
- r is the factor between the terms (called the "common ratio" )
Example: {1,2,4,8,...}
The sequence starts at 1 and doubles each time, so
- a=1 (the first term)
- r=2 (the "common ratio" between terms is a doubling)
And we get:
= {1, 1×2, 1×2 2 , 1×2 3 , ... }
= {1, 2, 4, 8, ... }
But be careful, r should not be 0:
- When r=0 , we get the sequence {a,0,0,...} which is not geometric
We can also calculate any term using the Rule:
x n = ar (n-1)
(We use "n-1" because ar 0 is for the 1st term)
Example: 10, 30, 90, 270, 810, 2430, ...
This sequence has a factor of 3 between each number.
The values of a and r are:
- a = 10 (the first term)
- r = 3 (the "common ratio")
The Rule for any term is:
x n = 10 × 3 (n-1)
So, the 4th term is:
x 4 = 10 × 3 (4-1) = 10 × 3 3 = 10 × 27 = 270
And the 10th term is:
x 10 = 10 × 3 (10-1) = 10 × 3 9 = 10 × 19683 = 196830
A Geometric Sequence can also have smaller and smaller values:
Example: 4, 2, 1, 0.5, 0.25, ...
This sequence has a factor of 0.5 (a half) between each number.
Its Rule is x n = 4 × (0.5) n-1
Why "Geometric" Sequence?
Because it is like increasing the dimensions in geometry :
Geometric Sequences are sometimes called Geometric Progressions (G.P.’s)
Summing a Geometric Series
To sum these:
a + ar + ar 2 + ... + ar (n-1)
(Each term is ar k , where k starts at 0 and goes up to n-1)
We can use this handy formula:
What is that funny Σ symbol? It is called Sigma Notation
And below and above it are shown the starting and ending values:
It says "Sum up n where n goes from 1 to 4. Answer= 10
The formula is easy to use ... just "plug in" the values of a , r and n
Example: Sum the first 4 terms of 10, 30, 90, 270, 810, 2430, ...
The values of a , r and n are:
- n = 4 (we want to sum the first 4 terms)
You can check it yourself:
10 + 30 + 90 + 270 = 400
And, yes, it is easier to just add them in this example , as there are only 4 terms.
But imagine adding 50 terms ... then the formula is much easier.
Using the Formula
Let's see the formula in action:
Example: Grains of Rice on a Chess Board
On the page Binary Digits we give an example of grains of rice on a chess board. The question is asked:
When we place rice on a chess board:
- 1 grain on the first square,
- 2 grains on the second square,
- 4 grains on the third and so on,
... doubling the grains of rice on each square ...
... how many grains of rice in total?
So we have:
- a = 1 (the first term)
- r = 2 (doubles each time)
- n = 64 (64 squares on a chess board)
= 1−2 64 −1 = 2 64 − 1
= 18,446,744,073,709,551,615
Which was exactly the result we got on the Binary Digits page (thank goodness!)
And another example, this time with r less than 1:
Example: Add up the first 10 terms of the Geometric Sequence that halves each time:
{ 1/2, 1/4, 1/8, 1/16, ... }.
- a = ½ (the first term)
- r = ½ (halves each time)
- n = 10 (10 terms to add)
Very close to 1.
(Question: if we continue to increase n , what happens?)
Why Does the Formula Work?
Let's see why the formula works, because we get to use an interesting "trick" which is worth knowing.
Notice that S and S·r are similar?
Now subtract them!
Wow! All the terms in the middle neatly cancel out. (Which is a neat trick)
By subtracting S·r from S we get a simple result:
S − S·r = a − ar n
Let's rearrange it to find S :
Which is our formula (ta-da!):
Infinite Geometric Series
So what happens when n goes to infinity ?
We can use this formula:
But be careful :
r must be between (but not including) −1 and 1
and r should not be 0 because the sequence {a,0,0,...} is not geometric
So our infnite geometric series has a finite sum when the ratio is less than 1 (and greater than −1)
Let's bring back our previous example, and see what happens:
Example: Add up ALL the terms of the Geometric Sequence that halves each time:
{ 1 2 , 1 4 , 1 8 , 1 16 , ... }.
= ½×1 ½ = 1
Yes, adding 1 2 + 1 4 + 1 8 + ... etc equals exactly 1 .
| Don't believe me? Just look at this square: By adding up + + + ... we end up with the whole thing! |
Recurring Decimal
On another page we asked "Does 0.999... equal 1?" , well, let us see if we can calculate it:
Example: Calculate 0.999...
We can write a recurring decimal as a sum like this:
And now we can use the formula:
Yes! 0.999... does equal 1.
So there we have it ... Geometric Sequences (and their sums) can do all sorts of amazing and powerful things.
12.3 Geometric Sequences and Series
Learning objectives.
By the end of this section, you will be able to:
- Determine if a sequence is geometric
- Find the general term (nth term) of a geometric sequence
- Find the sum of the first n n terms of a geometric sequence
- Find the sum of an infinite geometric series
- Apply geometric sequences and series in the real world
Be Prepared 12.7
Before you get started, take this readiness quiz.
Simplify: 24 32 . 24 32 . If you missed this problem, review Example 1.24 .
Be Prepared 12.8
Evaluate: ⓐ 3 4 3 4 ⓑ ( 1 2 ) 4 . ( 1 2 ) 4 . If you missed this problem, review Example 1.19 .
Be Prepared 12.9
If f ( x ) = 4 · 3 x , f ( x ) = 4 · 3 x , find ⓐ f ( 1 ) f ( 1 ) ⓑ f ( 2 ) f ( 2 ) ⓒ f ( 3 ) . f ( 3 ) . If you missed this problem, review Example 3.49 .
Determine if a Sequence is Geometric
We are now ready to look at the second special type of sequence, the geometric sequence.
A sequence is called a geometric sequence if the ratio between consecutive terms is always the same. The ratio between consecutive terms in a geometric sequence is r , the common ratio , where n is greater than or equal to two.
Geometric Sequence
A geometric sequence is a sequence where the ratio between consecutive terms is always the same.
The ratio between consecutive terms, a n a n − 1 , a n a n − 1 , is r , the common ratio . n is greater than or equal to two.
Consider these sequences.
Example 12.21
Determine if each sequence is geometric. If so, indicate the common ratio.
ⓐ 4 , 8 , 16 , 32 , 64 , 128 , … 4 , 8 , 16 , 32 , 64 , 128 , …
ⓑ −2 , 6 , −12 , 36 , −72 , 216 , … −2 , 6 , −12 , 36 , −72 , 216 , …
ⓒ 27 , 9 , 3 , 1 , 1 3 , 1 9 , … 27 , 9 , 3 , 1 , 1 3 , 1 9 , …
To determine if the sequence is geometric, we find the ratio of the consecutive terms shown.
| Find the ratio of the consecutive terms. | |
| The sequence is geometric. The common ratio is |
| Find the ratio of the consecutive terms. | |
| The sequence is not geometric. There is no common ratio. |
| Find the ratio of the consecutive terms. | |
| The sequence is geometric. The common ratio is |
Try It 12.41
Determine if each sequence is geometric. If so indicate the common ratio.
ⓐ 7 , 21 , 63 , 189 , 567 , 1,701 , … 7 , 21 , 63 , 189 , 567 , 1,701 , …
ⓑ 64 , 16 , 4 , 1 , 1 4 , 1 16 , … 64 , 16 , 4 , 1 , 1 4 , 1 16 , …
ⓒ 2 , 4 , 12 , 48 , 240 , 1,440 , … 2 , 4 , 12 , 48 , 240 , 1,440 , …
Try It 12.42
ⓐ −150 , −30 , −15 , −5 , − 5 2 , 0 , … −150 , −30 , −15 , −5 , − 5 2 , 0 , …
ⓑ 5 , 10 , 20 , 40 , 80 , 160 , … 5 , 10 , 20 , 40 , 80 , 160 , …
ⓒ 8 , 4 , 2 , 1 , 1 2 , 1 4 , … 8 , 4 , 2 , 1 , 1 2 , 1 4 , …
If we know the first term, a 1 , a 1 , and the common ratio, r , we can list a finite number of terms of the sequence.
Example 12.22
Write the first five terms of the sequence where the first term is 3 and the common ratio is r = −2 . r = −2 .
We start with the first term and multiply it by the common ratio. Then we multiply that result by the common ratio to get the next term, and so on.
The sequence is 3 , −6 , 12 , −24 , 48 , … 3 , −6 , 12 , −24 , 48 , …
Try It 12.43
Write the first five terms of the sequence where the first term is 7 and the common ratio is r = −3 . r = −3 .
Try It 12.44
Write the first five terms of the sequence where the first term is 6 and the common ratio is r = −4 . r = −4 .
Find the General Term ( n th Term) of a Geometric Sequence
Just as we found a formula for the general term of a sequence and an arithmetic sequence, we can also find a formula for the general term of a geometric sequence.
Let’s write the first few terms of the sequence where the first term is a 1 a 1 and the common ratio is r . We will then look for a pattern.
As we look for a pattern in the five terms above, we see that each of the terms starts with a 1 . a 1 .
The first term, a 1 , a 1 , is not multiplied by any r . In the second term, the a 1 a 1 is multiplied by r . In the third term, the a 1 a 1 is multiplied by r two times ( r · r r · r or r 2 r 2 ). In the fourth term, the a 1 a 1 is multiplied by r three times ( r · r · r r · r · r or r 3 r 3 ) and in the fifth term, the a 1 a 1 is multiplied by r four times. In each term, the number of times a 1 a 1 is multiplied by r is one less than the number of the term. This leads us to the following
General Term ( n th term) of a Geometric Sequence
The general term of a geometric sequence with first term a 1 a 1 and the common ratio r is
We will use this formula in the next example to find the fourteenth term of a sequence.
Example 12.23
Find the fourteenth term of a sequence where the first term is 64 and the common ratio is r = 1 2 . r = 1 2 .
| To find the fourteenth term, use the formula with and | |
| Substitute in the values. | |
| Simplify. | |
Try It 12.45
Find the thirteenth term of a sequence where the first term is 81 and the common ratio is r = 1 3 . r = 1 3 .
Try It 12.46
Find the twelfth term of a sequence where the first term is 256 and the common ratio is r = 1 4 . r = 1 4 .
Sometimes we do not know the common ratio and we must use the given information to find it before we find the requested term.
Example 12.24
Find the twelfth term of the sequence 3, 6, 12, 24, 48, 96, … Find the general term for the sequence.
To find the twelfth term, we use the formula, a n = a 1 r n − 1 , a n = a 1 r n − 1 , and so we need to first determine a 1 a 1 and the common ratio r .
| The first term is three. | |
| Find the common ratio. | |
| The common ratio is | |
| To find the twelfth term, use the formula with | |
| Substitute in the values. | |
| Simplify. | |
| Find the general term. | |
| We use the formula with |
Try It 12.47
Find the ninth term of the sequence 6, 18, 54, 162, 486, 1,458, … Then find the general term for the sequence.
Try It 12.48
Find the eleventh term of the sequence 7, 14, 28, 56, 112, 224, … Then find the general term for the sequence.
Find the Sum of the First n Terms of a Geometric Sequence
We found the sum of both general sequences and arithmetic sequence. We will now do the same for geometric sequences. The sum, S n , S n , of the first n terms of a geometric sequence is written as S n = a 1 + a 2 + a 3 + ... + a n . S n = a 1 + a 2 + a 3 + ... + a n . We can write this sum by starting with the first term, a 1 , a 1 , and keep multiplying by r to get the next term as:
Let’s also multiply both sides of the equation by r .
Next, we subtract these equations. We will see that when we subtract, all but the first term of the top equation and the last term of the bottom equation subtract to zero.
| We factor both sides. | |
| To obtain the formula for divide both sides by |
Sum of the First n Terms of a Geometric Series
The sum, S n , S n , of the first n terms of a geometric sequence is
where a 1 a 1 is the first term and r is the common ratio, and r is not equal to one.
We apply this formula in the next example where the first few terms of the sequence are given. Notice the sum of a geometric sequence typically gets very large when the common ratio is greater than one.

Example 12.25
Find the sum of the first 20 terms of the geometric sequence 7, 14, 28, 56, 112, 224, …
To find the sum, we will use the formula S n = a 1 ( 1 − r n ) 1 − r . S n = a 1 ( 1 − r n ) 1 − r . We know a 1 = 7 , a 1 = 7 , r = 2 , r = 2 , and n = 20 . n = 20 .
| Knowing and use the sum formula. | |
| Substitute in the values. | |
| Simplify. |
Try It 12.49
Find the sum of the first 20 terms of the geometric sequence 3, 6, 12, 24, 48, 96, …
Try It 12.50
Find the sum of the first 20 terms of the geometric sequence 6, 18, 54, 162, 486, 1,458, …
In the next example, we are given the sum in summation notation. While adding all the terms might be possible, most often it is easiest to use the formula to find the sum of the first n terms.
To use the formula, we need r . We can find it by writing out the first few terms of the sequence and find their ratio. Another option is to realize that in summation notation, a sequence is written in the form ∑ i = 1 k a ( r ) i , ∑ i = 1 k a ( r ) i , where r is the common ratio.
Example 12.26
Find the sum: ∑ i = 1 15 2 ( 3 ) i . ∑ i = 1 15 2 ( 3 ) i .
To find the sum, we will use the formula S n = a 1 ( 1 − r n ) 1 − r , S n = a 1 ( 1 − r n ) 1 − r , which requires a 1 a 1 and r . We will write out a few of the terms, so we can get the needed information.
| Write out the first few terms. | |
| Identify . | |
Find the common ratio. | |
Knowing and use the sum formula. | |
| Substitute in the values. | |
| Simplify. |
Try It 12.51
Find the sum: ∑ i = 1 15 6 ( 2 ) i . ∑ i = 1 15 6 ( 2 ) i .
Try It 12.52
Find the sum: ∑ i = 1 10 5 ( 2 ) i . ∑ i = 1 10 5 ( 2 ) i .
Find the Sum of an Infinite Geometric Series
If we take a geometric sequence and add the terms, we have a sum that is called a geometric series. An infinite geometric series is an infinite sum whose first term is a 1 a 1 and common ratio is r and is written
Infinite Geometric Series
An infinite geometric series is an infinite sum whose first term is a 1 a 1 and common ratio is r and is written
We know how to find the sum of the first n terms of a geometric series using the formula, S n = a 1 ( 1 − r n ) 1 − r . S n = a 1 ( 1 − r n ) 1 − r . But how do we find the sum of an infinite sum?
Let’s look at the infinite geometric series 3 + 6 + 12 + 24 + 48 + 96 + … . 3 + 6 + 12 + 24 + 48 + 96 + … . Each term gets larger and larger so it makes sense that the sum of the infinite number of terms gets larger. Let’s look at a few partial sums for this series. We see a 1 = 3 a 1 = 3 and r = 2 r = 2
As n gets larger and larger, the sum gets larger and larger. This is true when | r | ≥ 1 | r | ≥ 1 and we call the series divergent. We cannot find a sum of an infinite geometric series when | r | ≥ 1 . | r | ≥ 1 .
Let’s look at an infinite geometric series whose common ratio is a fraction less than one, 1 2 + 1 4 + 1 8 + 1 16 + 1 32 + 1 64 + … 1 2 + 1 4 + 1 8 + 1 16 + 1 32 + 1 64 + … . Here the terms get smaller and smaller as n gets larger. Let’s look at a few finite sums for this series. We see a 1 = 1 2 a 1 = 1 2 and r = 1 2 . r = 1 2 .
Notice the sum gets larger and larger but also gets closer and closer to one. When | r | < 1 , | r | < 1 , the expression r n r n gets smaller and smaller. In this case, we call the series convergent. As n approaches infinity, (gets infinitely large), r n r n gets closer and closer to zero. In our sum formula, we can replace the r n r n with zero and then we get a formula for the sum, S , for an infinite geometric series when | r | < 1 . | r | < 1 .
This formula gives us the sum of the infinite geometric sequence. Notice the S does not have the subscript n as in S n S n as we are not adding a finite number of terms.
Sum of an Infinite Geometric Series
For an infinite geometric series whose first term is a 1 a 1 and common ratio r ,
If | r | < 1 , the sum is If | r | < 1 , the sum is
If | r | ≥ 1 , the infinite geometric series does not have a sum. We say the series diverges. If | r | ≥ 1 , the infinite geometric series does not have a sum. We say the series diverges.
Example 12.27
Find the sum of the infinite geometric series 54 + 18 + 6 + 2 + 2 3 + 2 9 + … 54 + 18 + 6 + 2 + 2 3 + 2 9 + …
To find the sum, we first have to verify that the common ratio | r | < 1 | r | < 1 and then we can use the sum formula S = a 1 1 − r . S = a 1 1 − r .
| Find the common ratio. | |
| Identify | |
| Knowing use the sum formula. | |
| Substitute in the values. | |
| Simplify. |
Try It 12.53
Find the sum of the infinite geometric series 48 + 24 + 12 + 6 + 3 + 3 2 + … 48 + 24 + 12 + 6 + 3 + 3 2 + …
Try It 12.54
Find the sum of the infinite geometric series 64 + 16 + 4 + 1 + 1 4 + 1 16 + … 64 + 16 + 4 + 1 + 1 4 + 1 16 + …
An interesting use of infinite geometric series is to write a repeating decimal as a fraction.
Example 12.28
Write the repeating decimal 0. 5 – 0. 5 – as a fraction.
| Rewrite the showing the repeating five. | |
| Use place value to rewrite this as a sum. | |
| This is an infinite geometric series. | |
| Find the common ratio. | |
| Identify | |
| Knowing use the sum formula. | |
| Substitute in the values. | |
| Simplify. | |
| Multiply numerator and denominator by 10. | |
| We are asked to find the fraction form. |
Try It 12.55
Write the repeating decimal 0. 4 – 0. 4 – as a fraction.
Try It 12.56
Write the repeating decimal 0. 8 – 0. 8 – as a fraction.
Apply Geometric Sequences and Series in the Real World
One application of geometric sequences has to do with consumer spending. If a tax rebate is given to each household, the effect on the economy is many times the amount of the individual rebate.
Example 12.29
The government has decided to give a $1,000 tax rebate to each household in order to stimulate the economy. The government statistics say that each household will spend 80% of the rebate in goods and services. The businesses and individuals who benefitted from that 80% will then spend 80% of what they received and so on. The result is called the multiplier effect. What is the total effect of the rebate on the economy?
Every time money goes into the economy, 80% of it is spent and is then in the economy to be spent. Again, 80% of this money is spent in the economy again. This situation continues and so leads us to an infinite geometric series.
Here the first term is 1,000, a 1 = 1000 . a 1 = 1000 . The common ratio is 0.8 , 0.8 , r = 0.8 . r = 0.8 . We can evaluate this sum since 0.8 < 1 . 0.8 < 1 . We use the formula for the sum on an infinite geometric series.
| Substitute in the values, and | |
| Evaluate. |
The total effect of the $1,000 received by each household will be a $5,000 growth in the economy.
Try It 12.57
What is the total effect on the economy of a government tax rebate of $1,000 to each household in order to stimulate the economy if each household will spend 90% of the rebate in goods and services?
Try It 12.58
What is the total effect on the economy of a government tax rebate of $500 to each household in order to stimulate the economy if each household will spend 85% of the rebate in goods and services?
We have looked at a compound interest formula where a principal, P , is invested at an interest rate, r , for t years. The new balance, A , is A = P ( 1 + r n ) n t A = P ( 1 + r n ) n t when interest is compounded n times a year. This formula applies when a lump sum was invested upfront and tells us the value after a certain time period.
An annuity is an investment that is a sequence of equal periodic deposits. We will be looking at annuities that pay the interest at the time of the deposits. As we develop the formula for the value of an annuity, we are going to let n = 1 . n = 1 . That means there is one deposit per year.
| Let | |
| Simplify. |
Suppose P dollars is invested at the end of each year. One year later that deposit is worth P ( 1 + r ) 1 P ( 1 + r ) 1 dollars, and another year later it is worth P ( 1 + r ) 2 P ( 1 + r ) 2 dollars. After t years, it will be worth A = P ( 1 + r ) t A = P ( 1 + r ) t dollars.
| End of year 1 | End of year 2 | End of year 3 | |
|---|---|---|---|
| First Deposit @ end of year 1 | Amount 1 year later | Amount 2 years later | |
| 2nd Deposit @ end of year 2 | Amount 1 year later | ||
| 3 Deposit @ end of year 3 |
After three years, the value of the annuity is
This a sum of the terms of a geometric sequence where the first term is P and the common ratio is 1 + r . 1 + r . We substitute these values into the sum formula. Be careful, we have two different uses of r . The r in the sum formula is the common ratio of the sequence. In this case, that is 1 + r 1 + r where r is the interest rate.
| Substitute in the values. | |
| Simplify. | |
Remember our premise was that one deposit was made at the end of each year.
We can adapt this formula for n deposits made per year and the interest is compounded n times a year.
Value of an Annuity with Interest Compounded n n Times a Year
For a principal, P , invested at the end of a compounding period, with an interest rate, r , which is compounded n times a year, the new balance, A, after t years, is
Example 12.30
New parents decide to invest $100 per month in an annuity for their baby daughter. The account will pay 5% interest per year which is compounded monthly. How much will be in the child’s account at her eighteenth birthday?
To find the Annuity formula, A t = P ( ( 1 + r n ) n t − 1 ) r n , A t = P ( ( 1 + r n ) n t − 1 ) r n , we need to identify P , r , n , and t .
| Identify , the amount invested each month. | |
| Identify , the annual interest rate, in decimal form. | |
| Identify , the number of times the deposit will be made and the interest compounded each year. | |
| Identify , the number of years. | |
| Knowing use the sum formula. | |
| Substitute in the values. | |
| Use the calculator to evaluate. Be sure to use parentheses as needed. | |
| The child will have $34,920.20 when she turns 18. |
Try It 12.59
New grandparents decide to invest $200 per month in an annuity for their grandson. The account will pay 5% interest per year which is compounded monthly. How much will be in the child’s account at his twenty-first birthday?
Try It 12.60
Arturo just got his first full-time job after graduating from college at age 27. He decided to invest $200 per month in an IRA (an annuity). The interest on the annuity is 8%, which is compounded monthly. How much will be in the Arturo’s account when he retires at his sixty-seventh birthday?
Access these online resources for additional instruction and practice with sequences.
- Geometric Sequences
- Geometric Series
- Future Value Annuities and Geometric Series
- Application of a Geometric Series: Tax Rebate
Section 12.3 Exercises
Practice makes perfect.
In the following exercises, determine if the sequence is geometric, and if so, indicate the common ratio.
3 , 12 , 48 , 192 , 768 , 3072 , … 3 , 12 , 48 , 192 , 768 , 3072 , …
2 , 10 , 50 , 250 , 1250 , 6250 , … 2 , 10 , 50 , 250 , 1250 , 6250 , …
72 , 36 , 18 , 9 , 9 2 , 9 4 , … 72 , 36 , 18 , 9 , 9 2 , 9 4 , …
54 , 18 , 6 , 2 , 2 3 , 2 9 , … 54 , 18 , 6 , 2 , 2 3 , 2 9 , …
−3 , 6 , −12 , 24 , −48 , 96 , … −3 , 6 , −12 , 24 , −48 , 96 , …
2 , −6 , 18 , −54 , 162 , −486 , … 2 , −6 , 18 , −54 , 162 , −486 , …
In the following exercises, determine if each sequence is arithmetic, geometric or neither. If arithmetic, indicate the common difference. If geometric, indicate the common ratio.
48 , 24 , 12 , 6 , 3 , 3 2 , … 48 , 24 , 12 , 6 , 3 , 3 2 , …
12 , 6 , 0 , −6 , −12 , −18 , … 12 , 6 , 0 , −6 , −12 , −18 , …
−7 , −2 , 3 , 8 , 13 , 18 , … −7 , −2 , 3 , 8 , 13 , 18 , …
5 , 9 , 13 , 17 , 21 , 25 , … 5 , 9 , 13 , 17 , 21 , 25 , …
1 2 , 1 4 , 1 8 , 1 16 , 1 32 , 1 64 , … 1 2 , 1 4 , 1 8 , 1 16 , 1 32 , 1 64 , …
4 , 8 , 12 , 24 , 48 , 96 , … 4 , 8 , 12 , 24 , 48 , 96 , …
In the following exercises, write the first five terms of each geometric sequence with the given first term and common ratio.
a 1 = 4 a 1 = 4 and r = 3 r = 3
a 1 = 9 a 1 = 9 and r = 2 r = 2
a 1 = −4 a 1 = −4 and r = −2 r = −2
a 1 = −5 a 1 = −5 and r = −3 r = −3
a 1 = 27 a 1 = 27 and r = 1 3 r = 1 3
a 1 = 64 a 1 = 64 and r = 1 4 r = 1 4
In the following exercises, find the indicated term of a sequence where the first term and the common ratio is given.
Find a 11 a 11 given a 1 = 8 a 1 = 8 and r = 3 . r = 3 .
Find a 13 a 13 given a 1 = 7 a 1 = 7 and r = 2 . r = 2 .
Find a 10 a 10 given a 1 = −6 a 1 = −6 and r = −2 . r = −2 .
Find a 15 a 15 given a 1 = −4 a 1 = −4 and r = −3 . r = −3 .
Find a 10 a 10 given a 1 = 100,000 a 1 = 100,000 and r = 0.1 . r = 0.1 .
Find a 8 a 8 given a 1 = 1,000,000 a 1 = 1,000,000 and r = 0.01 . r = 0.01 .
In the following exercises, find the indicated term of the given sequence. Find the general term for the sequence.
Find a 9 a 9 of the sequence, 9 , 18 , 36 , 72 , 144 , 288 , … 9 , 18 , 36 , 72 , 144 , 288 , …
Find a 12 a 12 of the sequence, 5 , 15 , 45 , 135 , 405 , 1215 , … 5 , 15 , 45 , 135 , 405 , 1215 , …
Find a 15 a 15 of the sequence, −486 , 162 , −54 , 18 , −6 , 2 , … −486 , 162 , −54 , 18 , −6 , 2 , …
Find a 16 a 16 of the sequence, 224 , −112 , 56 , −28 , 14 , −7 , … 224 , −112 , 56 , −28 , 14 , −7 , …
Find a 10 a 10 of the sequence, 1 , 0.1 , 0.01 , 0.001 , 0.0001 , 0.00001 , … 1 , 0.1 , 0.01 , 0.001 , 0.0001 , 0.00001 , …
Find a 9 a 9 of the sequence, 1000 , 100 , 10 , 1 , 0.1 , 0.01 , … 1000 , 100 , 10 , 1 , 0.1 , 0.01 , …
Find the Sum of the First n terms of a Geometric Sequence
In the following exercises, find the sum of the first fifteen terms of each geometric sequence.
8 , 24 , 72 , 216 , 648 , 1944 , … 8 , 24 , 72 , 216 , 648 , 1944 , …
7 , 14 , 28 , 56 , 112 , 224 , … 7 , 14 , 28 , 56 , 112 , 224 , …
−6 , 12 , −24 , 48 , −96 , 192 , … −6 , 12 , −24 , 48 , −96 , 192 , …
−4 , 12 , −36 , 108 , −324 , 972 , … −4 , 12 , −36 , 108 , −324 , 972 , …
81 , 27 , 9 , 3 , 1 , 1 3 , … 81 , 27 , 9 , 3 , 1 , 1 3 , …
256 , 64 , 16 , 4 , 1 , 1 4 , 1 16 , … 256 , 64 , 16 , 4 , 1 , 1 4 , 1 16 , …
In the following exercises, find the sum of the geometric sequence.
∑ i = 1 15 ( 2 ) i ∑ i = 1 15 ( 2 ) i
∑ i = 1 10 ( 3 ) i ∑ i = 1 10 ( 3 ) i
∑ i = 1 9 4 ( 2 ) i ∑ i = 1 9 4 ( 2 ) i
∑ i = 1 8 5 ( 3 ) i ∑ i = 1 8 5 ( 3 ) i
∑ i = 1 10 9 ( 1 3 ) i ∑ i = 1 10 9 ( 1 3 ) i
∑ i = 1 15 4 ( 1 2 ) i ∑ i = 1 15 4 ( 1 2 ) i
In the following exercises, find the sum of each infinite geometric series.
1 + 1 3 + 1 9 + 1 27 + 1 81 + 1 243 + 1 729 + … 1 + 1 3 + 1 9 + 1 27 + 1 81 + 1 243 + 1 729 + …
1 + 1 2 + 1 4 + 1 8 + 1 16 + 1 32 + 1 64 + … 1 + 1 2 + 1 4 + 1 8 + 1 16 + 1 32 + 1 64 + …
6 − 2 + 2 3 − 2 9 + 2 27 − 2 81 + … 6 − 2 + 2 3 − 2 9 + 2 27 − 2 81 + …
−4 + 2 − 1 + 1 2 − 1 4 + 1 8 − … −4 + 2 − 1 + 1 2 − 1 4 + 1 8 − …
6 + 12 + 24 + 48 + 96 + 192 + … 6 + 12 + 24 + 48 + 96 + 192 + …
5 + 15 + 45 + 135 + 405 + 1215 + … 5 + 15 + 45 + 135 + 405 + 1215 + …
1,024 + 512 + 256 + 128 + 64 + 32 + … 1,024 + 512 + 256 + 128 + 64 + 32 + …
6,561 + 2187 + 729 + 243 + 81 + 27 + … 6,561 + 2187 + 729 + 243 + 81 + 27 + …
In the following exercises, write each repeating decimal as a fraction.
0. 3 – 0. 3 –
0. 6 – 0. 6 –
0. 7 – 0. 7 –
0. 2 – 0. 2 –
0. 45 — 0. 45 —
0. 27 — 0. 27 —
In the following exercises, solve the problem.
Find the total effect on the economy of each government tax rebate to each household in order to stimulate the economy if each household will spend the indicated percent of the rebate in goods and services.
| Tax rebate to each household | Percent spent on goods and services | Total Effect on the economy | |
|---|---|---|---|
| ⓐ | |||
| ⓑ | |||
| ⓒ | |||
| ⓓ |
New grandparents decide to invest $ 100 $ 100 per month in an annuity for their grandchild. The account will pay 6 % 6 % interest per year which is compounded monthly (12 times a year). How much will be in the child’s account at their twenty-first birthday?
Berenice just got her first full-time job after graduating from college at age 30. She decided to invest $ 500 $ 500 per quarter in an IRA (an annuity). The interest on the annuity is 7 % 7 % which is compounded quarterly (4 times a year). How much will be in the Berenice’s account when she retires at age 65?
Alice wants to purchase a home in about five years. She is depositing $ 500 $ 500 a month into an annuity that earns 5 % 5 % per year that is compounded monthly (12 times a year). How much will Alice have for her down payment in five years?
Myra just got her first full-time job after graduating from college. She plans to get a master’s degree, and so is depositing $ 2,500 $ 2,500 a year from her year-end bonus into an annuity. The annuity pays 6.5 % 6.5 % per year and is compounded yearly. How much will she have saved in five years to pursue her master’s degree?
Writing Exercises
In your own words, explain how to determine whether a sequence is geometric.
In your own words, explain how to find the general term of a geometric sequence.
In your own words, explain the difference between a geometric sequence and a geometric series.
In your own words, explain how to determine if an infinite geometric series has a sum and how to find it.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
- Authors: Lynn Marecek, Andrea Honeycutt Mathis
- Publisher/website: OpenStax
- Book title: Intermediate Algebra 2e
- Publication date: May 6, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
- Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/12-3-geometric-sequences-and-series
© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Geometric Sequence & Applications
These lessons help High School students to express and interpret geometric sequence applications.
Related Pages Number Sequences Linear Sequences Geometric Sequences: n-th Term Quadratic and Cubic Sequences
Examples, solutions, videos, and lessons to help High School students learn to choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.
A. Factor a quadratic expression to reveal the zeros of the function it defines.
B. Complete the square in a quadratic expression to reveal the maximum or minimum value of the function it defines.
C. Use the properties of exponents to transform expressions for exponential functions. For example, the expression 1.15 t can be rewritten as (1.15 1/12 ) 12t ≈ 1.012 12t to reveal the approximate equivalent monthly interest rate if the annual rate is 15%.
Suggested Learning Targets
Use properties of exponents (such as power of a power, product of powers, power of a product, and rational exponents, etc.) to write an equivalent form of an exponential function to reveal and explain specific information about its approximate rate of growth or decay.
Common Core: HSA-SSE.B.3c
Geometric Sequences Word Problems
- Bruno has 3 pizza stores and wants to dramatically expand his franchise nationwide. If the number of stores he owns doubles in number each month, what month will he launch 6,144 stores?
- On January 1, Abby’s troop sold three boxes of Girl Scout cookies online. Their daily goal is to sell double the number of boxes as the previous day. At this rate, how many boxes will they sell on day 7? If this pattern continues, on what day will they sell 24,576 boxes of cookies?
Compounding Interest and other Geometric Sequence Word Problems
- Suppose you invest $1,000 in the bank. You leave the money in for 3 years, each year getting 5% interest per annum. How much money do you have in the bank after 3 years?
- You invest $5000 for 20 years at 2% p.a. How much will we end up with? How does this change if the interest is given quarterly? monthly?
- If I can invest at 5% and I want $50,000 in 10 years, how much should I invest now?
- I decide to run a rabbit farm. I have 50 rabbits. The rabbit grows at 7% per week. How many will I have in 15 weeks?
Geometric sequence - salary
Example: You land a job as a police officer. Your salary for the first year is $43,125. You will receive 7% increase every year. How much will your salary be at the start of year six?
Solve Word Problems using Geometric Sequences
Example: Wilma bought a house for $170,000. Each year, it increases 2% of its value. a. Write the equation that represents the house’s value over time. b. What will the house be worth in 10 years?
Application of a Geometric Sequence
Example: Bouncing ball application of a geometric sequence When a ball is dropped onto a flat floor, it bounces to 65% of the height from which it was dropped. If the ball is dropped from 80 cm, find the height of the fifth bounce.
Population Growth and Compound Interest
This video gives examples of population growth and compound interest. Remember these examples are variations on geometric sequence.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
- + ACCUPLACER Mathematics
- + ACT Mathematics
- + AFOQT Mathematics
- + ALEKS Tests
- + ASVAB Mathematics
- + ATI TEAS Math Tests
- + Common Core Math
- + DAT Math Tests
- + FSA Tests
- + FTCE Math
- + GED Mathematics
- + Georgia Milestones Assessment
- + GRE Quantitative Reasoning
- + HiSET Math Exam
- + HSPT Math
- + ISEE Mathematics
- + PARCC Tests
- + Praxis Math
- + PSAT Math Tests
- + PSSA Tests
- + SAT Math Tests
- + SBAC Tests
- + SIFT Math
- + SSAT Math Tests
- + STAAR Tests
- + TABE Tests
- + TASC Math
- + TSI Mathematics
- + ACT Math Worksheets
- + Accuplacer Math Worksheets
- + AFOQT Math Worksheets
- + ALEKS Math Worksheets
- + ASVAB Math Worksheets
- + ATI TEAS 6 Math Worksheets
- + FTCE General Math Worksheets
- + GED Math Worksheets
- + 3rd Grade Mathematics Worksheets
- + 4th Grade Mathematics Worksheets
- + 5th Grade Mathematics Worksheets
- + 6th Grade Math Worksheets
- + 7th Grade Mathematics Worksheets
- + 8th Grade Mathematics Worksheets
- + 9th Grade Math Worksheets
- + HiSET Math Worksheets
- + HSPT Math Worksheets
- + ISEE Middle-Level Math Worksheets
- + PERT Math Worksheets
- + Praxis Math Worksheets
- + PSAT Math Worksheets
- + SAT Math Worksheets
- + SIFT Math Worksheets
- + SSAT Middle Level Math Worksheets
- + 7th Grade STAAR Math Worksheets
- + 8th Grade STAAR Math Worksheets
- + THEA Math Worksheets
- + TABE Math Worksheets
- + TASC Math Worksheets
- + TSI Math Worksheets
- + AFOQT Math Course
- + ALEKS Math Course
- + ASVAB Math Course
- + ATI TEAS 6 Math Course
- + CHSPE Math Course
- + FTCE General Knowledge Course
- + GED Math Course
- + HiSET Math Course
- + HSPT Math Course
- + ISEE Upper Level Math Course
- + SHSAT Math Course
- + SSAT Upper-Level Math Course
- + PERT Math Course
- + Praxis Core Math Course
- + SIFT Math Course
- + 8th Grade STAAR Math Course
- + TABE Math Course
- + TASC Math Course
- + TSI Math Course
- + Number Properties Puzzles
- + Algebra Puzzles
- + Geometry Puzzles
- + Intelligent Math Puzzles
- + Ratio, Proportion & Percentages Puzzles
- + Other Math Puzzles
How to Solve Geometric Sequences? (+FREE Worksheet!)
Learn how to solve Geometric Sequence problems using the following step-by-step guide with detailed solutions.

Related Topics
- How to Solve Finite Geometric Series
- How to Solve Infinite Geometric Series
- How to Solve Arithmetic Sequences
Step by step guide to solve Geometric Sequence Problems
- It is a sequence of numbers where each term after the first is found by multiplying the previous item by the common ratio, a fixed, non-zero number. For example, the sequence \(2, 4, 8, 16, 32\), … is a geometric sequence with a common ratio of \(2\).
- To find any term in a geometric sequence use this formula: \(\color{blue}{x_{n}=ar^{(n – 1)}}\)
- \(a =\) the first term , \(r =\) the common ratio , \(n =\) number of items
Geometric Sequences – Example 1:
Given the first term and the common ratio of a geometric sequence find the first five terms of the sequence. \(a_1=3,r=-2\)
Use geometric sequence formula: \(\color{blue}{x_{n}=ar^{(n – 1)}}\) \(→x_{n}=0.8 .(-5)^{n-1}\) If \(n=1\) then: \(x_{1}=3 .(-2)^{1-1}=3 (1)=3\), First Five Terms: \(3,-6,12,-24,48\)
The Absolute Best Books to Ace Pre-Algebra to Algebra II
The Ultimate Algebra Bundle From Pre-Algebra to Algebra II
Geometric sequences – example 2:.
Given two terms in a geometric sequence find the 8th term. \(a_{3}=10\) and \(a_{5}=40\)
Use geometric sequence formula: \(\color{blue}{x_{n}=ar^{(n – 1)}}\) \(→a_{3}=ar^{(3 – 1)}=ar^2=10\) \(x_{n}=ar^{(n – 1)}→a_5=ar^{(5 – 1)}=ar^4=40\) Now divide \(a_{5}\) by \(a_{3}\). Then: \(\frac{a_{5}}{a_{3}} =\frac{ar^4}{ar^2 }=\frac{40}{10}\), Now simplify: \(\frac{ar^4}{ar^2 }=\frac{40}{10}→r^2=4→r=2\) We can find a now: \(ar^2=12→a(2^2 )=10→a=2.5\) Use the formula to find the 8th term: \(x_{n}=ar^{(n – 1)}→a_8=(2.5) (2)^8=2.5(256)=640\)
Geometric Sequences – Example 3:
Given the first term and the common ratio of a geometric sequence find the first five terms of the sequence. \(a_{1}=0.8,r=-5\)
Use geometric sequence formula: \(\color{blue}{x_{n}=ar^{(n – 1)}}\) \(→x_{n}=0.8 .(-5)^{n-1}\) If \(n=1\) then: \(x_{1}=0.8 .(-5)^{1-1}=0.8 (1)=0.8\), First Five Terms: \(0.8,-4,20,-100,500\)
The Best Book to Help You Ace Pre-Algebra
Pre-Algebra for Beginners The Ultimate Step by Step Guide to Preparing for the Pre-Algebra Test
Geometric sequences – example 4:.
Given two terms in a geometric sequence find the 8th term. \(a_3=12\) and \(a_5=48\)
Use geometric sequence formula: \(\color{blue}{x_{n}=ar^{(n – 1)}}\) \(→a_3=ar^{(3 – 1)}=ar^2=12\) \(\color{blue}{x_{n}=ar^{(n – 1)}}\) \(→a_5=ar^{(5 – 1)}=ar^4=48\) Now divide \(a_{5}\) by \(a_{3}\). Then: \(\frac{a_{5}}{a_{3} }=\frac{ar^4}{ar^2}=\frac{48}{12}\), Now simplify: \(\frac{ar^4}{ar^2}=\frac{48}{12}→r^2=4→r=2\) We can find a now: \(ar^2=12→a(2^2 )=12→a=3\) Use the formula to find the \(8^{th}\) term: \(\color{blue}{x_{n}=ar^{(n – 1)}}\) \(→a_{8}=(3) (2)^8=3(256)=768\)
Exercises for Solving Geometric Sequences
Determine if the sequence is geometric. if it is, find the common ratio..
- \(\color{blue}{1, – 5, 25, – 125, …}\)
- \(\color{blue}{– 2, – 4, – 8, – 16, …}\)
- \(\color{blue}{4, 16, 36, 64, …}\)
- \(\color{blue}{– 3, – 15, – 75, – 375, …}\)
Download Geometric Sequences Worksheet
- \(\color{blue}{r=-5}\)
- \(\color{blue}{r=2}\)
- \(\color{blue}{not \ geometric}\)
- \(\color{blue}{r=5}\)
The Greatest Books for Students to Ace the Algebra
Pre-Algebra Exercise Book A Comprehensive Workbook + PreAlgebra Practice Tests
Pre-algebra in 10 days the most effective pre-algebra crash course, college algebra practice workbook the most comprehensive review of college algebra, high school algebra i a comprehensive review and step-by-step guide to mastering high school algebra 1, 10 full length clep college algebra practice tests the practice you need to ace the clep college algebra test.
by: Effortless Math Team about 4 years ago (category: Articles , Free Math Worksheets )
Effortless Math Team
Related to this article, more math articles.
- How to Graph Functions
- How to Write Slope-intercept Form and Point-slope Form?
- The Ultimate 6th Grade GMAS Math Course (+FREE Worksheets)
- Journey to the Land of Proportions: How to Write and Solve Equations Utilizing Proportional Relationships
- Overview of the TExES Core Subjects Mathematics Test
- 10 Most Common 6th Grade Common Core Math Questions
- Top 10 ACT Math Prep Books (Our 2023 Favorite Picks)
- Full-Length DAT Quantitative Reasoning Practice Test-Answers and Explanations
- How to Navigate Inequalities: The Impact of Addition and Subtraction on Fractional Values
- FREE SSAT Middle Level Math Practice Test
What people say about "How to Solve Geometric Sequences? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.
Leave a Reply Cancel reply
You must be logged in to post a comment.
Pre-Algebra Practice Workbook The Most Comprehensive Review of Pre-Algebra
Algebra i practice workbook the most comprehensive review of algebra 1, algebra ii practice workbook the most comprehensive review of algebra 2, algebra i for beginners the ultimate step by step guide to acing algebra i, algebra ii for beginners the ultimate step by step guide to acing algebra ii, pre-algebra tutor everything you need to help achieve an excellent score.
- ATI TEAS 6 Math
- ISEE Upper Level Math
- SSAT Upper-Level Math
- Praxis Core Math
- 8th Grade STAAR Math
Limited time only!
Save Over 45 %
It was $89.99 now it is $49.99
Login and use all of our services.
Effortless Math services are waiting for you. login faster!
Register Fast!
Password will be generated automatically and sent to your email.
After registration you can change your password if you want.
- Math Worksheets
- Math Courses
- Math Topics
- Math Puzzles
- Math eBooks
- GED Math Books
- HiSET Math Books
- ACT Math Books
- ISEE Math Books
- ACCUPLACER Books
- Premium Membership
- Youtube Videos
Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.
- Bulk Orders
- Refund Policy

Geometric Sequence
Geometric sequence formula.
A geometric sequence (also known as geometric progression) is a type of sequence wherein every term except the first term is generated by multiplying the previous term by a fixed nonzero number called common ratio , r.
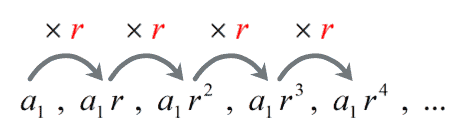
More so, if we take any term in the geometric sequence except the first term and divide it by the previous term, the quotient is always the same. This constant or fixed quotient is called the common ratio and is usually represented by the letter r.
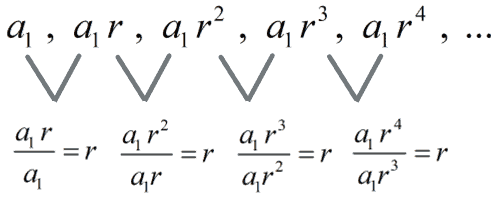
How to “Derive” the Geometric Sequence Formula
To generate a geometric sequence, we start by writing the first term. Then we multiply the first term by a fixed nonzero number to get the second term of the geometric sequence.
To obtain the third sequence, we take the second term and multiply it by the common ratio. Maybe you are seeing the pattern now. To get to the next term of the sequence, you multiply the preceding term by the constant nonzero number that we used as the common multiplier.
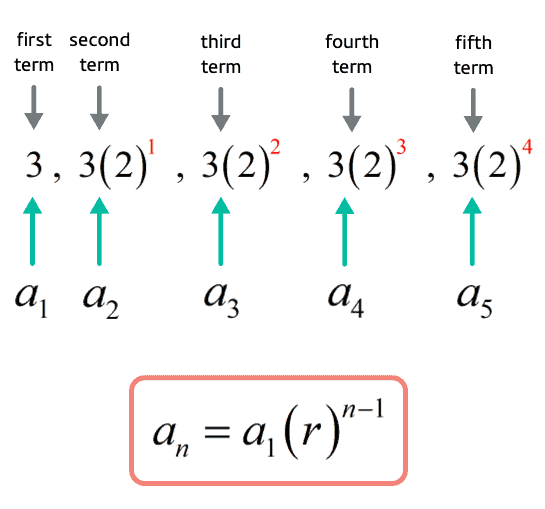
To make a sense of this all, let’s have a concrete example. Suppose we have a geometric sequence wherein
the first term , [latex]\large{a_1}[/latex], is 3
the fixed constant or common ratio , [latex]\large{r}[/latex], is 2 .
So if the first term is [latex]3[/latex] then we have
[latex]\large{{a_1} = 3}[/latex]
The second term is generated by multiplying the first term by the fixed constant [latex]2[/latex].
[latex]\large{{a_2} = 3\left( 2 \right)^1}[/latex]
The third term is generated by multiplying the second term by the fixed constant [latex]2[/latex].
[latex]\large{{a_3} = 3\left( 2 \right)\left( 2 \right) = 3{\left( 2 \right)^2}}[/latex]
The fourth term is obtained by multiplying the third term by the fixed constant [latex]2[/latex].
[latex]\large{{a_4} = 3\left( 2 \right)\left( 2 \right)\left( 2 \right) = 3{\left( 2 \right)^3}}[/latex]
The fifth term is obtained by multiplying the fourth term by the fixed constant [latex]2[/latex].
[latex]\large{{a_5} = 3\left( 2 \right)\left( 2 \right)\left( 2 \right)\left( 2 \right) = 3{\left( 2 \right)^4}}[/latex]
So now how can we interpret and use the example above to convert it into a formula? Observe that the first term [latex]\color{red}\large{{a_1}}[/latex] is always present in every term of the sequence. In the same manner, the fixed constant [latex]\color{red}\large{r}[/latex] is also attached in every term to some power. Notice that
- if [latex]\large{n}[/latex] is [latex]1[/latex] the power of [latex]\large{r}[/latex] is [latex]0[/latex]
- if [latex]\large{n}[/latex] is [latex]2[/latex] the power of [latex]\large{r}[/latex] is [latex]1[/latex]
- if [latex]\large{n}[/latex] is [latex]3[/latex] the power of [latex]\large{r}[/latex] is [latex]2[/latex]
- if [latex]\large{n}[/latex] is [latex]4[/latex] the power of [latex]\large{r}[/latex] is [latex]3[/latex]
- if [latex]\large{n}[/latex] is [latex]5[/latex] the power of [latex]\large{r}[/latex] is [latex]4[/latex]
Note: [latex]\large{n}[/latex] is the subscript of [latex]\large{a}[/latex] as in [latex]\large{a_n}[/latex]
It means that the power of the fixed constant (also known as the common ratio) [latex]\color{red}\large{r}[/latex] is [latex]1[/latex] less than whatever [latex]\large{n}[/latex] is.
Therefore, we can now deduce that the nth term [latex]\color{red}\large{{a_n}}[/latex] of a geometrc sequence is equal to the first term [latex]\color{red}\large{{a_1}}[/latex] multiplied to the fixed constant (also known as the common ratio) [latex]\color{red}\large{{r}}[/latex] raised to 1 less than [latex]\large{{n}}[/latex].
[latex]\LARGE{{a_n} = {a_1}{\left( r \right)^{n – 1}}}[/latex]
Below is a quick illustration on how we derive the geometric sequence formula.
Breakdown of the Geometric Sequence Formula

Notes about the geometric sequence formula:
- the common ratio r cannot be zero
- n is the position of the term in the sequence. For example, the third term is [latex]n=3[/latex], the fourth term is [latex]n=4[/latex], the fifth term is [latex]n=5[/latex], and so on.
Examples of Using the Geometric Sequence Formula
To learn and get familiar with the formula quickly, we will start with easy or foundational problems then gradually progress to more challenging ones. Feel free to skip the problems that you already know and jump to the ones that you want to go over.
Example 1: Tell whether each sequence is geometric or not. Explain.
a) Sequence A: [latex]3,12,48,192,…[/latex]
b) Sequence B: [latex] – 1,2, – 4,8,…[/latex]
c) Sequence C: [latex]4,8,12,16,…[/latex]
d) Sequence D: [latex]\Large{{1 \over 3},{1 \over 2},{3 \over 4},{9 \over 8},…}[/latex]
a) Yes. Sequence A is a geometric sequence because there is a common ratio between consecutive terms. The common ratio is [latex]4[/latex].
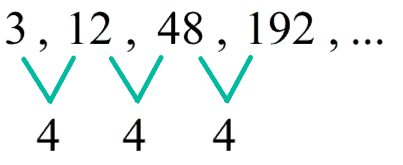
b) Yes. Sequence B is also a geometric sequence since the adjacent terms have a common ratio which is [latex]-2[/latex].
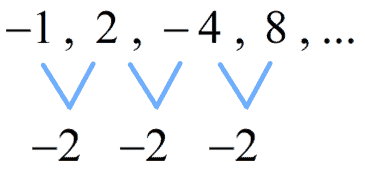
Notice that when a geometric sequence has a negative common ratio, the sequence will have alternating signs. That means the signs of the terms are switching back and forth between positive and negative.
c) No. Sequence C is not a geometric sequence. The consecutive terms don’t have a common ratio.
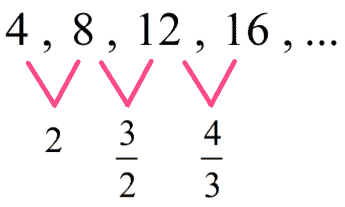
I hope you recognize that this is another kind of sequence. Notice, there is a common difference between consecutive terms which is [latex]4[/latex]. That is,
[latex]8-4=4[/latex]
[latex]12-8=4[/latex]
[latex]16-12=4[/latex]
Since the common difference is [latex]4[/latex], this is in fact an arithmetic sequence .
d) Yes. Sequence D is a geometric sequence because it has a common ratio of [latex]\Large{{3 \over 2}}[/latex].
Remember that when we divide fractions, we convert the problem from division to multiplication. Take the dividend (fraction being divided) and multiply it to the reciprocal of the divisor. Then, we simplify as needed.
[latex]\Large{{1 \over 2} \div {1 \over 3} = {1 \over 2} \times {3 \over 1} = {3 \over 2}}[/latex]
[latex]\Large{{3 \over 4} \div {1 \over 2} = {3 \over 4} \times {2 \over 1} = {3 \over 2}}[/latex]
[latex]\Large{{9 \over 8} \div {3 \over 4} = {9 \over 8} \times {4 \over 3} = {3 \over 2}}[/latex]
Example 2: Write a geometric sequence with five (5) terms wherein the first term is [latex]0.5[/latex] and the common ratio is [latex]6[/latex].
The first term is given to us which is [latex]\large{{a_1} = 0.5}[/latex]. Thus, we will have to find the other four terms. We can use the common ratio to produce the next four terms. The common ratio which in this case is [latex]6[/latex] will serve as the fixed multiplier to calculate the rest of the terms in the sequence.
The first term is [latex]{0.5}[/latex]. The second term is the first term multiplied by the common ratio [latex]6[/latex] which equals [latex]3[/latex]. The third term is the second term times [latex]6[/latex], and so on.
[latex]\large{{a_1} = 0.5}[/latex]
[latex]\large{{a_2} = 0.5\left( 6 \right) = 3}[/latex]
[latex]\large{{a_3} = 3\left( 6 \right) = 18}[/latex]
[latex]\large{{a_4} = 18\left( 6 \right) = 108}[/latex]
[latex]\large{{a_5} = 108\left( 6 \right) = 648}[/latex]
Therefore, the geometric sequence that satisfies the given conditions is
[latex]{0.5\,\,,\,\,3\,\,,\,\,18\,\,,\,\,\,108\,\,,\,\,648\,\,,\,\,…}[/latex]
Example 3: Generate a geometric sequence with five (5) terms such that each term is half the previous term. Answers may vary.
There is an infinite number of geometric sequences that can satisfy this condition because we are not restricted to a particular first term. We can use any numbers as our first term. That’s why the answers to this problem will vary as we are free to choose our starting term.
The problem can be expressed algebraically as
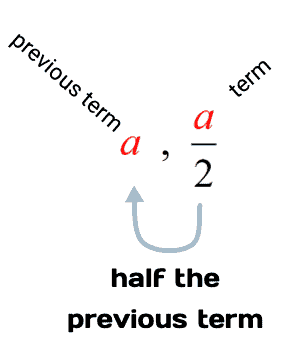
It only means that to go from the previous term to the following term, we multiply the previous term by [latex]\Large{{1 \over 2}}[/latex] to get to the next.
If we pick [latex]48[/latex] as our first term, we multiply it by [latex]\Large{{1 \over 2}}[/latex] to produce the second term. To generate the third term, multiply the second term by [latex]\Large{{1 \over 2}}[/latex], and so on.
[latex]\large{{a_1} = 48}[/latex]
[latex]\large{{a_2} = 48\left( {{1 \over 2}} \right) = 24}[/latex]
[latex]\large{{a_3} = 24\left( {{1 \over 2}} \right) = 12}[/latex]
[latex]\large{{a_4} = 12\left( {{1 \over 2}} \right) = 6}[/latex]
[latex]\large{{a_5} = 6\left( {{1 \over 2}} \right) = 3}[/latex]
So here’s our geometric sequence with five (5) terms such that each term (except the first term) is one-half of the previous term.
[latex]\large{48\,,\,\,24\,\,,\,\,12\,\,,\,\,6\,\,,\,\,3\,\,,\,\,…}[/latex]
Example 4: The first term of the geometric sequence is [latex]7[/latex] while its common ratio is [latex]-2[/latex]. Write the nth term formula of the sequence in the standard form.
The standard formula of the geometric sequence is

This is an easy problem because the values of the first term and the common ratio are given to us. We simply substitute them into the formula and we are done.
Since [latex]{a_1} = 7[/latex] and [latex]r = – 2[/latex], we have
[latex]\large{{a_n} = 7{\left( { – 2} \right)^{n – 1}}}[/latex]
Example 5: Determine the nth term formula of the geometric sequence below.
[latex]\large{16\,,\,\,12\,\,,\,\,9\,\,,\,\,…}[/latex]
To write the nth term formula, we will need the values of the first term and the common ratio. Since we are given the geometric sequence itself, the first term [latex]\large{{a_1}}[/latex] can easily be found.
The first term of the geometric sequence is obviously [latex]16[/latex].

Divide each term by the previous term. Since the quotients are the same, then it becomes our common ratio. In this case, we have [latex]\Large{r = {3 \over 4}}[/latex].
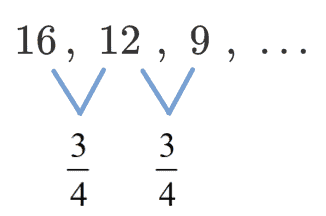
Substituting the values of the first term and the common ratio into the formula, we get
[latex]\Large{{a_n} = {a_1}{\left( r \right)^{n – 1}}}[/latex]
[latex]\Large{{a_n} = 16{\left( {{3 \over 4}} \right)^{n – 1}}}[/latex]
Example 6: Determine the indicated terms below using the geometric sequence formula.
a) The first term is [latex]3[/latex]. Find the sixth term if the common ratio is [latex]2[/latex].
b) The first term is [latex]-2[/latex]. Find the seventh term if the common ratio is [latex]-3[/latex].
Solution: These two (2) problems are very similar. The first term and the common ratio are both given in the problem. The only thing we have to do is to plug these values into the geometric sequence formula then use it to find the nth term of the sequence.
a) The first term is [latex]\large{{a_1} = 3}[/latex] while its common ratio is [latex]r = 2[/latex].
This gives us

To find the sixth term, we let [latex]n=6[/latex] then simplify.
[latex]\large{a_n} = 3{\left( 2 \right)^{n – 1}}[/latex]
[latex]\large{a_6} = 3{\left( 2 \right)^{6 – 1}}[/latex]
[latex]\large = 3{\left( 2 \right)^5}[/latex]
[latex]\large = 3\left( {32} \right)[/latex]
[latex]\large{a_6} = 96[/latex]
b) The first term is [latex]\large{{a_1} = -2}[/latex] and the common ratio is [latex]r = -3[/latex].
The nth term formula becomes

To find the seventh term, we will set [latex]n=7[/latex] then simplify.
[latex]\large{a_n} = – 2{\left( { – 3} \right)^{n – 1}}[/latex]
[latex]\large{a_7} = – 2{\left( { – 3} \right)^{7 – 1}}[/latex]
[latex]\large = – 2{\left( { – 3} \right)^6}[/latex]
[latex]\large = – 2\left( {729} \right)[/latex]
[latex]\large {a_7} = – 1,458[/latex]
Example 7: Find the tenth term of the geometric sequence below.
[latex]\Large{1 \over 3}\,\,,\,\,\,1\,\,,\,\,\,3\,\,,\,\,\,9\,\,,\,\,…[/latex]
This problem is similar to example 6. The only difference is that the values of the first term and common ratio are not given upfront. However, they can easily be found and computed from the geometric sequence.
The very first term of the sequence is very obvious to identify.

Calculate the common ratio by dividing each term by the previous term. If the quotients are the same, then it is our common ratio.

Since the first term is [latex]\large{a_1} = {1 \over 3}[/latex] and the common ratio is [latex]r = 3[/latex], we write the general formula as
[latex]\Large{a_n} = {1 \over 3}{\left( 3 \right)^{n – 1}}[/latex]
The 10th term is calculated by letting [latex]n=10[/latex].
[latex]\Large{a_{10}} = {1 \over 3}{\left( 3 \right)^{10 – 1}}[/latex]
[latex]\Large = {1 \over 3}{\left( 3 \right)^9}[/latex]
[latex]\large = {1 \over 3}\left( {19,683} \right)[/latex]
[latex]\large {a_{10}} = 6,561[/latex]
Example 8: The second term of a geometric sequence is [latex]2[/latex], and the fifth term is [latex]\Large{1 \over {32}}[/latex]. Find the ninth term.
We will use the given two terms to create a system of equations that we can solve to find the common ratio [latex]r[/latex] and the first term [latex]{a_1}[/latex]. After doing so, it is possible to write the general formula that can find any term in the geometric sequence. In particular, we want to find the ninth term.
Since [latex]\large{a_2} = 2[/latex] and [latex]\large{a_5} = {1 \over {32}}[/latex], we substitute them in the nth term formula [latex]\large{a_n} = {a_1}{\left( r \right)^{n – 1}}[/latex] to get
Equation 1:
[latex]\large2 = {a_1}r[/latex]
Equation 2:
[latex]\Large{{1 \over {32}} = {a_1}{r^4}}[/latex]
Let’s divide equation 2 by equation 1 to cancel the variable [latex]\large{a_1}[/latex]. What’s left is an equation that we can solve for [latex]\large{r}[/latex].
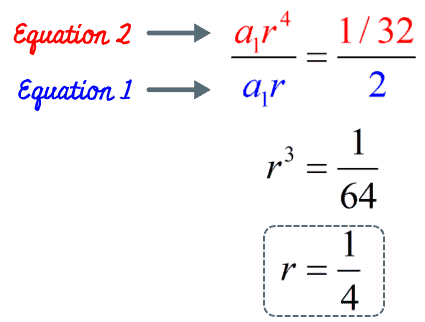
We can now solve for the value of the first term by substituting the value of [latex]r[/latex] to either equation 1 or 2 then solve for [latex]\large{a_1}[/latex]. We will use equation 1 because it is much simpler.
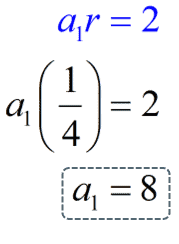
This gives us the nth term formula of the geometric sequence.

Finally, we can solve for the 9th term of the geometric sequence by letting [latex]n=9[/latex] and simplifying it.
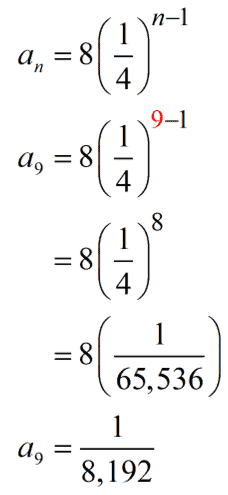
Example 9: The third term of a geometric sequence is [latex]5[/latex], and the seventh term is [latex]\Large{5 \over {16}}[/latex]. Find the thirteenth term.
I’m sure that you already know the drill. We will use the information of the given two terms from the problem to create a system of equations with [latex]\color{red}\large{a_1}[/latex] and [latex]\color{red}r[/latex] as the unknown variables.
For [latex]\large{a_3=5}[/latex], our equation 1 is
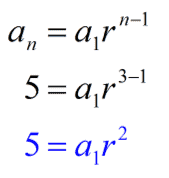
For [latex]\large{a_7} = {5 \over {16}}[/latex], our equation 2 is
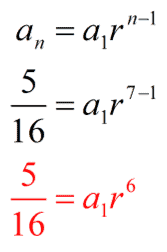
We divide equation 2 by equation 1 to cancel out the [latex]\large{a_1}[/latex] term then solve for [latex]\large{r}[/latex].
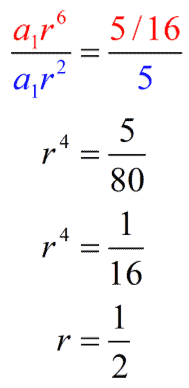
Now, we solve for [latex]\large{a_1}[/latex] by substituting the value of [latex]r=1/2[/latex] to any of the equations. We will use equation 1 because it is the simpler one of the two.
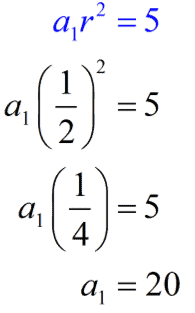
We can now put together the nth term formula of the geometric sequence.
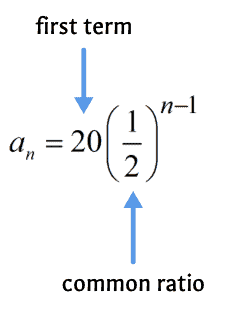
Finally, we solve the value of the missing term. Since we are looking for the 13th term of the geometric sequence, we let [latex]n=13[/latex] then simplify.
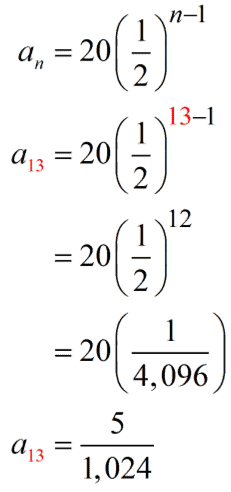
You may also be interested in these related math lessons or tutorials:
Geometric Series Formula
Geometric Series Practice Problems
Arithmetic Sequence Formula
Arithmetic Sequence Practice Problems with Answers
Arithmetic Series Formula
Arithmetic Series Formula Practice Problems
- Français

- No results found.
- Preparatory
Lesson Explainer: Applications of Geometric Sequences and Series Mathematics • Second Year of Secondary School
In this explainer, we will learn how to solve real-world applications of geometric sequences and series, where we will find the common ratio, the 𝑛 t h term explicit formula, the order and value of a specific sequence term, and the sum of a given number of terms.
Let us consider a sequence where each term is found by multiplying the previous term by a constant. For example, the sequence 2 , 6 , 1 8 , 5 4 , 1 6 2 , 4 8 6 , … .
We call this constant multiplier the common ratio. Another way to describe the sequence would be to say that each term in the sequence is equal to the previous term multiplied by the common ratio.
This is known as a geometric sequence, in this case with a first term equal to 2 and a common ratio of 3. If our sequence just consisted of, say, the six terms above (or indeed any specific number of terms), then we call it a finite geometric sequence, because it has a finite number of terms. If the sequence followed this pattern forever, as the ellipsis at the end implies, then we call it an infinite geometric sequence.
Definition: Geometric Sequence
A geometric sequence is a sequence that has a common ratio, 𝑟 , between consecutive terms. The first term is denoted by 𝑇 or 𝑇 , the second term 𝑇 , the third term 𝑇 , and so on. The 𝑛 t h term is denoted by 𝑇 .
Each term is found by multiplying the previous term by the common ratio: 𝑇 = 𝑇 , 𝑇 = 𝑇 × 𝑟 , 𝑇 = 𝑇 × 𝑟 , … , 𝑇 = 𝑇 × 𝑟 .
This can also be expressed as the first term multiplied by powers of the common ratio: 𝑇 = 𝑇 , 𝑇 = 𝑇 𝑟 , 𝑇 = 𝑇 𝑟 , … such that the 𝑛 t h term is defined by 𝑇 = 𝑇 𝑟 .
Returning to our initial geometric sequence above, if we know the numbers in the sequence, we can calculate the common ratio by dividing the value of one term by the value of the previous term. Since the ratio is common between all successive pairs of terms, it does not matter which pair we choose for our calculation.
The ratio of the first two terms is 6 ÷ 2 = 3 , the ratio of the second two terms is 1 8 ÷ 6 = 3 , and so on.
Definition: The Common Ratio
Since we multiply one term by the common ratio to get the next term, we can express this generally as 𝑇 = 𝑇 × 𝑟 , and by dividing both sides of the equation by 𝑇 , we get 𝑟 = 𝑇 𝑇 .
Alternatively, with the definition that any term is the result of multiplying the previous term by the common ratio, we find that 𝑟 = 𝑇 𝑇 .
The sum of the terms in a sequence is called a series. Given the geometric sequence ( 2 , 6 , 1 8 , 5 4 , 1 6 2 , 4 8 6 , 1 4 5 8 , 4 3 7 4 , 1 3 1 2 2 , 3 9 3 6 6 , … ) , the corresponding geometric series could be represented as follows: 2 + 6 + 1 8 + 5 4 + 1 6 2 + 4 8 6 + 1 4 5 8 + 4 3 7 4 + 1 3 1 2 2 + 3 9 3 6 6 + ⋯ .
In this case, by adding together the first 10 terms in the series, we can see that the sum of these terms is 59 048 .
We will now derive a formula for the sum of the first 𝑛 terms of geometric sequence.
Consider a geometric sequence with first term 𝑇 and common ratio 𝑟 . The first 𝑛 terms can be written as 𝑇 , 𝑇 𝑟 , 𝑇 𝑟 , … , 𝑇 𝑟 , so the sum of the first 𝑛 terms of a geometric sequence can be written as follows:
If we multiply both sides of our equation by 𝑟 , we have
When we subtract the terms in equation (2) from the terms in equation (1), all but the terms 𝑇 and 𝑇 𝑟 cancel out: 𝑆 = 𝑇 + 𝑇 𝑟 + 𝑇 𝑟 + ⋯ + 𝑇 𝑟 + 𝑇 𝑟 , 𝑟 𝑆 = 𝑇 𝑟 + 𝑇 𝑟 + 𝑇 𝑟 + ⋯ + 𝑇 𝑟 + 𝑇 𝑟 .
So, 𝑆 − 𝑟 𝑆 = 𝑇 − 𝑇 𝑟 .
Factoring 𝑆 from the right-hand side and 𝑇 from the left-hand side will allow us to create an equation for 𝑆 : 𝑆 ( 1 − 𝑟 ) = 𝑇 ( 1 − 𝑟 ) 𝑆 = 𝑇 ( 1 − 𝑟 ) 1 − 𝑟 .
Alternatively, we could have subtracted (1) from equation (2) to obtain the formula 𝑆 = 𝑇 ( 𝑟 − 1 ) 𝑟 − 1 .
Definition: The Sum of a Finite Geometric Sequence
The sum of the first 𝑛 terms of a geometric sequence, with first term 𝑇 and common ratio 𝑟 , is denoted by 𝑆 : 𝑆 = 𝑇 ( 1 − 𝑟 ) 1 − 𝑟 𝑆 = 𝑇 ( 𝑟 − 1 ) 𝑟 − 1 . o r
Generally, we use the first version when 𝑟 1 and the second one when 𝑟 > 1 .
If 𝑟 = 1 , all the terms of the geometric sequence are the same, so we would just need to multiply the first term by the number of terms: 𝑆 = 𝑇 × 𝑛 .
We will now look at how we can apply some of the above formulae to solve real-world problems involving geometric sequences and series.
Example 1: Solving an Applied Problem Using Geometric Sequences
Amira joined a company with a starting salary of $ 28 000 . She receives a 2 . 5 % salary increase after each full year in the job.
- The total Amira earns over 𝑛 years is a geometric series. What is the common ratio?
- Write a formula for 𝑆 , the total amount in dollars that Amira earns in 𝑛 years at the company.
- After 20 years with the company, Amira leaves. Use your formula to calculate the total amount she earned there.
- Explain why the actual amount she earned will be different from the amount calculated using the formula.
- She spent part of the money within the 20 years .
- The value of the dollar varies with time.
- When necessary, the new annual salary will be rounded.
- The actual amount will have a different percentage compared to the amount calculated using the formula.
- The actual amount will have a different starting value compared to the amount calculated using the formula.
There are four parts to this question that we will work through individually.
We are given that Amira has a starting salary of $ 28 000 and that she receives a salary increase of 2 . 5 % after each full year in the job. This is enough information to determine that the amount she earns in 𝑛 years will be a geometric sequence. The first part of this question asks us to calculate the common ratio of this series.
When we talk about the ratio of a geometric series, we mean the ratio of the geometric sequence that makes up that series.
Any geometric sequence can be written in the form 𝑇 , 𝑇 𝑟 , 𝑇 𝑟 , … , 𝑇 𝑟 , where 𝑇 is the first term and 𝑟 is the common ratio. We can calculate the common ratio by calculating the quotient of two successive terms: 𝑟 = 𝑇 𝑇 .
We know that in year 1 , Amira will earn $ 28 000 . In year 2, she will have had a 2 . 5 % salary increase. We can therefore calculate the amount of money Amira earns in year 2 by calculating 2 . 5 % of $ 28 000 and then adding this value on.
An alternative method here would be to use the multiplier method. As Amira’s salary is increasing by 2 . 5 % , we need to multiply her salary be 1.025.
In year 2, she will earn $ 2 8 0 0 0 × 1 . 0 2 5 = $ 2 8 7 0 0 .
This is enough to find the common ratio as we can see that the first term 𝑇 = $ 2 8 0 0 0 and the common ratio 𝑟 = 1 . 0 2 5 .
We could, however, continue this pattern to show how much money Amira earns in year 3, year 4, and so on:
- Y e a r 1 = $ 2 8 0 0 0
- Y e a r 2 = $ 2 8 0 0 0 × 1 . 0 2 5
- Y e a r 3 = $ 2 8 0 0 0 × 1 . 0 2 5 × 1 . 0 2 5 = $ 2 8 0 0 0 × 1 . 0 2 5
- Y e a r 4 = $ 2 8 0 0 0 × 1 . 0 2 5 × 1 . 0 2 5 × 1 . 0 2 5 = $ 2 8 0 0 0 × 1 . 0 2 5
This means that in the 𝑛 t h year Amira will earn $ 2 8 0 0 0 × 1 . 0 2 5 , as the exponent or power will always be 1 less than the number of years .
This ties in with our general expression for the 𝑛 t h term of a geometric sequence 𝑇 = 𝑇 𝑟 .
The common ratio of the sequence is 1.025.
In the second part of the question, we need to write a formula for 𝑆 , the total amount of dollars that Amira earns in 𝑛 years at the company.
We know that the sum of the first 𝑛 terms of a geometric series, denoted 𝑆 , can be found using the following formula: 𝑆 = 𝑇 ( 𝑟 − 1 ) 𝑟 − 1 .
Substituting 𝑇 = 2 8 0 0 0 and 𝑟 = 1 . 0 2 5 , we have 𝑆 = 2 8 0 0 0 ( 1 . 0 2 5 − 1 ) 1 . 0 2 5 − 1 𝑆 = 2 8 0 0 0 ( 1 . 0 2 5 − 1 ) 0 . 0 2 5 𝑆 = 1 1 2 0 0 0 0 ( 1 . 0 2 5 − 1 ) .
The formula for 𝑆 , the total amount of dollars that Amira earns in 𝑛 years at the company, is 𝑆 = 1 1 2 0 0 0 0 ( 1 . 0 2 5 − 1 ) .
In order to calculate the amount of money Amira will have earned after 20 years at the company, we need to substitute 𝑛 = 2 0 into our previous answer: 𝑆 = 1 1 2 0 0 0 0 1 . 0 2 5 − 1 𝑆 = 7 1 5 2 5 0 . 4 1 .
When Amira leaves the company after 20 years , she will have earned $ 715 250.41 , to the nearest cent.
The final part of the question asks us why the actual amount she earned will be different from the amount calculated using the formula. There are five possible answer options to this part of the question.
This is an interesting problem, and we will consider each option one at a time.
While it is true that Amira will probably have spent some of her money in the 20- year period, this would not affect the amount of money she earned, only the amount of money she had left. Therefore, option A is not the correct answer.
It is true that the value of the dollar would have changed over time; however, as Amira was always paid in dollars throughout this period, the value of the dollar will have no impact on the amount that Amira earns. Option B is also incorrect.
The third option presents an interesting problem that we come across regularly in mathematics: when to round our answers. When we use the formula to calculate the total amount that Amira earned, we use exact values for years 1–20 and only round the answer at the end. However, in reality, the salary would be rounded in each year . For example, in year 4, Amira earned $ 2 8 0 0 0 × 1 . 0 2 5 = $ 3 0 1 5 2 . 9 3 7 5 . This would be rounded to the nearest cent, so Amira actually earned $ 30 152.94 . As a result, when we add these rounded values, we will obtain a slightly different value than when using the formula. This is true of any problem when dealing in currency as these values have to be rounded to two decimal places.
Options D and E suggest that there will be a different percentage and a different starting value; however, neither of these statements are true as the percentage increase in salary is always 2 . 5 % and the starting salary is always $ 28 000 . Both of these answers are therefore incorrect.
The actual amount Amira earned will be different from the amount calculated using the formula, because when necessary, the new annual salary will be rounded. The correct answer is option C.
Example 2: Modeling a Real-World Problem Using a Geometric Sequence and Using It to Solve a Problem
A gold mine produced 2 257 kg in the first year but production decreased by 1 4 % annually. Find the amount of gold produced in the third year and the total across all 3 years . Give the answers to the nearest kilogram .
We need to calculate the amount of gold produced in the 3rd year and the total amount produced across all three years . One way of doing this would be to directly find these values from the information given in the question.
We are told that the amount of gold produced in the first year is 2 257 kg .
In the second year , there is a 1 4 % decrease. We could calculate 1 4 % of 2 257 kg and then subtract this value from 2 257 kg . Alternatively, we could multiply 2 257 kg by ( 1 − 0 . 1 4 ) , as 1 4 % written as a decimal is 0.14. This gives us a multiplier equal to 0.86.
These methods only really work when we need to calculate a small number of years .
If we needed to calculate over a longer period of time, we can use our knowledge of geometric sequences. We know that any geometric sequence has a first term 𝑇 and common ratio 𝑟 .
The amount of gold produced by the mine forms such a sequence, where 𝑇 = 2 2 5 7 and 𝑟 = 0 . 8 6 . We know that the common ratio, 𝑟 , is 0.86 as this is the constant that we multiply each term by to get the next term.
The general term of a geometric sequence, 𝑇 , can be calculated using the formula 𝑇 = 𝑇 𝑟 . Substituting in our values, we have 𝑇 = 2 2 5 7 ( 0 . 8 6 ) = 2 2 5 7 ( 0 . 8 6 ) = 1 6 6 9 . 2 7 7 2 .
Once again, we see that the amount of gold produced in the third year is equal to 1 669 kg , rounded to the nearest kilogram .
The sum of the first 𝑛 terms of a geometric sequence 𝑆 can be calculated using the formula 𝑆 = 𝑇 ( 1 − 𝑟 ) 1 − 𝑟 . Substituting in our values, we have 𝑆 = 2 2 5 7 1 − 0 . 8 6 1 − 0 . 8 6 𝑆 = 2 2 5 7 1 − 0 . 8 6 0 . 1 4 𝑆 = 5 8 6 7 . 2 9 7 2 .
The total amount of gold produced across all three years is equal to 5 867 kg , rounded to the nearest kilogram .
In the next example, we will consider the situation when an amount of money is invested into a savings account where an annual interest rate is compounded monthly.
Example 3: Solving a Finance Problem Where Interest Is Compounded Monthly Using Geometric Sequences
Sameh saves $20 every month in an account that pays an annual interest rate of 4 % compounded monthly.
- How much will be in Sameh’s account after 4 years of regular saving? Give your answer to the nearest cent.
- If the interest was compounded quarterly, how much would be in the account after 4 years ?
There are two parts to this question both of which can be modeled using geometric sequences.
Firstly, we have an account that pays an annual interest rate of 4 % compounded monthly, so the monthly rate can be calculated by dividing 4 % by 12: m o n t h l y i n t e r e s t r a t e = 0 . 0 4 1 2 = 1 3 0 0 .
The multiplier will therefore be equal to 1 + 1 3 0 0 = 3 0 1 3 0 0 , so the common ratio 𝑟 = 3 0 1 3 0 0 .
Sameh saves $20 every month , so the first term of the geometric sequence 𝑇 = $ 2 0 .
Over the four- year period, there will be 4 × 1 2 = 4 8 monthly payments, which means there are 48 terms in our geometric sequence, so 𝑛 = 4 8 .
The sum of the first 𝑛 terms of a geometric sequence, 𝑆 , can be calculated using the formula 𝑆 = 𝑇 ( 𝑟 − 1 ) 𝑟 − 1 . Substituting in our values, we have 𝑆 = 2 0 − 1 − 1 𝑆 = 1 0 3 9 . 1 9 2 0 … .
Rounding this to two decimal places, we can conclude that there is $ 1 039.19 in Sameh’s account after 4 years .
Secondly, we have an account that pays an annual interest rate of 4 % compounded quarterly, so the quarterly rate can be calculated by dividing 4 % by 4: q u a r t e r l y i n t e r e s t r a t e = 0 . 0 4 4 = 1 1 0 0 .
The multiplier will therefore be equal to 1 + 1 1 0 0 = 1 0 1 1 0 0 , so the common ratio 𝑟 = 1 0 1 1 0 0 .
Sameh saves $20 every month , so each quarter he will have saved 3 × $ 2 0 = $ 6 0 ; therefore, the first term of the geometric sequence 𝑇 = $ 6 0 .
Over the four- year period there will be 16 quarterly payments, which means there are 16 terms in our geometric sequence, so 𝑛 = 1 6 .
The sum of the first 𝑛 terms of a geometric sequence, 𝑆 , can be calculated using the formula 𝑆 = 𝑇 ( 𝑟 − 1 ) 𝑟 − 1 . Substituting in our values, we have 𝑆 = 6 0 − 1 − 1 𝑆 = 1 0 3 5 . 4 7 1 8 … .
Rounding this to two decimal places, we can conclude that there is $ 1 035.47 in Sameh’s account after 4 years .
We can therefore conclude that if the interest is compounded monthly rather than quarterly, then Sameh will earn more interest across the four- year term.
In our final example we will solve another real-world problem involving geometric sequences.
Example 4: Solving a Physical Problem Involving Volume Using Geometric Sequences
A water tank had 1 778 litres of water. The volume of the water decreased by 14, 28, and 56 litres over the next three days respectively. How long will it take the tank to be empty given that the water volume decreases following the same pattern?
We notice that the values 1 4 , 2 8 , 5 6 , … form a geometric sequence, with first term 𝑇 = 1 4 and common ratio 𝑟 = 2 . To check this, we divide each term by the term before it: 5 6 ÷ 2 8 = 2 8 ÷ 1 4 = 2 .
The sum of the first 𝑛 terms of a geometric sequence, 𝑆 , can be calculated using the formula 𝑆 = 𝑇 ( 𝑟 − 1 ) 𝑟 − 1 .
Since the total amount of water in the tank is 1 778 litres , then 𝑆 = 1 7 7 8 and we want to calculate the time period, 𝑛 , in days .
Substituting in our values we have 1 7 7 8 = 1 4 ( 2 − 1 ) 2 − 1 1 7 7 8 = 1 4 ( 2 − 1 ) ( 1 4 ) 1 2 7 = 2 − 1 ( 1 ) 1 2 8 = 2 . d i v i d i n g b o t h s i d e s b y a d d i n g t o b o t h s i d e s
We know that 128 is a power of 2, so 𝑛 is an integer value.
In fact, 2 is 128, so 𝑛 = 7 .
Note that this can also be solved using logarithms, although this is outside the scope of this explainer.
Therefore, the water tank will be empty after 7 days .
We can verify this answer by calculating the amount of water in the tank at the end of each day by subtracting 1 4 , 2 8 , 5 6 , … individually.
End of day 1: 1 7 7 8 − 1 4 = 1 7 6 4
End of day 2: 1 7 6 4 − 2 8 = 1 7 3 6
End of day 3: 1 7 3 6 − 5 6 = 1 6 8 0
End of day 4: 1 6 8 0 − 1 1 2 = 1 5 6 8
End of day 5: 1 5 6 8 − 2 2 4 = 1 3 4 4
End of day 6: 1 3 4 4 − 4 4 8 = 8 9 6
End of day 7: 8 9 6 − 8 9 6 = 0
This confirms that the water tank will be empty after 7 days .
We will finish this explainer by recapping some of the key points.
- Many real-world problems involve geometric sequences and series. The following definitions can help us solve these problems.
- A finite geometric sequence has the form 𝑇 , 𝑇 𝑟 , 𝑇 𝑟 , … , 𝑇 𝑟 , where 𝑇 is the first term, 𝑟 is the common ratio, and 𝑛 is the number of terms in the sequence.
- The 𝑛 t h term of a geometric sequence is 𝑇 = 𝑇 𝑟 .
- The common ratio 𝑟 of a geometric sequence whose 𝑛 t h term is 𝑇 is given by 𝑟 = 𝑇 𝑇 or 𝑟 = 𝑇 𝑇 .
- The sum of the terms in a sequence is called a series.
- The sum of the first 𝑛 terms of a geometric sequence, with first term 𝑇 and common ratio 𝑟 , is denoted by 𝑆 , where 𝑆 = 𝑇 ( 1 − 𝑟 ) 1 − 𝑟 𝑆 = 𝑇 ( 𝑟 − 1 ) 𝑟 − 1 . o r
Join Nagwa Classes
Attend live sessions on Nagwa Classes to boost your learning with guidance and advice from an expert teacher!
- Interactive Sessions
- Chat & Messaging
- Realistic Exam Questions
- macOS Apple Silicon
- macOS Intel

Nagwa uses cookies to ensure you get the best experience on our website. Learn more about our Privacy Policy
- Pre-algebra lessons
- Pre-algebra word problems
- Algebra lessons
- Algebra word problems
- Algebra proofs
- Advanced algebra
- Geometry lessons
- Geometry word problems
- Geometry proofs
- Trigonometry lessons
- Consumer math
- Baseball math
- Math for nurses
- Statistics made easy
- High school physics
- Basic mathematics store
- SAT Math Prep
- Math skills by grade level
- Ask an expert
- Other websites
- K-12 worksheets
- Worksheets generator
- Algebra worksheets
- Geometry worksheets
- Free math problem solver
- Pre-algebra calculators
- Algebra Calculators
- Geometry Calculators
- Math puzzles
- Math tricks
- Member login
Geometric sequence word problems
This lesson will show you how to solve a variety of geometric sequence word problems.
Example #1:
The stock's price of a company is not doing well lately. Suppose the stock's price is 92% of its previous price each day. What is the stock's price after 10 days if the stock was worth $2500 right before it started to go down?
To solve this problem, we need the geometric sequence formula shown below.
a n = a 1 × r (n - 1)
a 1 = original value of the stock = 2500
a 2 = value of the stock after 1 day
a 11 = value of the stock after 10 days
a 11 = 2500 × (0.92) (11 - 1)
a 11 = 2500 × (0.92) 10
a 11 = 2500 × 0.434
a 11 = $1085
The stock's price is about 1085 dollars.
Example #2:
The third term of a geometric sequence is 45 and the fifth term of the geometric sequence is 405. If all the terms of the sequence are positive numbers, find the 15th term of the geometric sequence.
Solution To solve this problem, we need the geometric sequence formula shown below.
a n = a 1 × r (n - 1)
Find the third term
a 3 = a 1 × r (3 - 1)
a 3 = a 1 × r 2
Since the third term is 45, 45 = a 1 × r 2 ( equation 1 )
Find the fifth term
a 5 = a 1 × r (5 - 1)
a 5 = a 1 × r 4
Since the fifth term is 405, 405 = a 1 × r 4 ( equation 2 )
Divide equation 2 by equation 1 .
(a 1 × r 4 ) / (a 1 × r 2 ) = 405 / 45
Cancel a 1 since it is both on top and at the bottom of the fraction.
r 4 / r 2 = 9
r = ±√9
r = ±3
Use r = 3, and equation 1 to find a 1
45 = a 1 × (3) 2
45 = a 1 × 9
a 1 = 45 / 9 = 5
Since all the terms of the sequence are positive numbers, we must use r = 3 if we want all the terms to be positive numbers.
Let us now find a 15
a 15 = 5 × (3) (15 - 1)
a 15 = 5 × (3) 14
a 15 = 5 × 4782969
a 15 = 23914845
Challenging geometric sequence word problems
Example #3:
Suppose that the magnification of a PDF file on a desktop computer is increased by 15% for each level of zoom. Suppose also that the original length of the word " January " is 1.2 cm. Find the length of the word " January " after 6 magnifications.
a 1 = original length of the word = 1.2 cm
a 2 = length of the word after 1 magnification
a 7 = length of the word after 6 magnifications
r = 1 + 0.15 = 1.15
a 7 = 1.2 × (1.15) (7 - 1)
a 7 = 1.2 × (1.15) 6
a 7 = 1.2 × 2.313
a 7 = 2.7756
After 6 magnifications, the length of the word "January" is 2.7756 cm.
Notice that we added 1 to 0.15. Why did we do that? Let us not use the formula directly so you can see the reason behind it. Study the following carefully !
Day 1 : a 1 = 1.2
Day 2 : a 2 = 1.2 + 1.2 (0.15) = 1.2 (1 + 0.15)
Day 3 : a 3 = 1.2(1 + 0.15) + [ 1.2(1 + 0.15) ]0.15 = 1.2(1 + 0.15) (1 + 0.15) = 1.2(1 + 0.15) 2
Day 7 : a 7 = 1.2(1 + 0.15) 6
Suppose that you want a reduced copy of a photograph. The actual length of the photograph is 10 inches. If each reduction is 64% of the original, how many reductions, will shrink the photograph to 1.07 inches.
a 1 = original length of the photograph = 10 inches
a 2 = length of the photograph after 1 reduction
n = number of reductions = ?
1.07 = 10 × (0.64) (n - 1)
Divide both sides by 10
1.07 / 10 = [10 × (0.64) (n - 1) ] / 10
0.107 = (0.64) (n - 1)
Notice that you have an exponential equation to solve. The biggest challenge then is knowing how to solve exponential equations !
Take the natural log of both sides of the equation.
ln(0.107) = ln[(0.64) (n - 1) ]
Use the power property of logarithms .
ln(0.107) = (n - 1)ln(0.64)
Divide both sides of the equation by ln(0.64)
ln(0.107) / ln(0.64) = (n - 1)ln(0.64) / ln(0.64)
n - 1 = ln(0.107) / ln(0.64)
Use a calculator to find ln(0.107) and ln(0.64)
n - 1 = -2.23492644452 \ -0.44628710262
n - 1 = 5.0078
n = 1 + 5.0078
Therefore, you will need 6 reductions.
Geometric sequence
Arithmetic sequence word problems
Recent Articles
How to divide any number by 5 in 2 seconds.
Feb 28, 24 11:07 AM
Math Trick to Square Numbers from 50 to 59
Feb 23, 24 04:46 AM
Sum of Consecutive Odd Numbers
Feb 22, 24 10:07 AM
100 Tough Algebra Word Problems. If you can solve these problems with no help, you must be a genius!

Recommended
About me :: Privacy policy :: Disclaimer :: Donate Careers in mathematics
Copyright © 2008-2021. Basic-mathematics.com. All right reserved

- HW Guidelines
- Study Skills Quiz
- Find Local Tutors
- Demo MathHelp.com
- Join MathHelp.com
Select a Course Below
- ACCUPLACER Math
- Math Placement Test
- PRAXIS Math
- + more tests
- 5th Grade Math
- 6th Grade Math
- Pre-Algebra
- College Pre-Algebra
- Introductory Algebra
- Intermediate Algebra
- College Algebra
Arithmetic & Geometric Sequences
Intro Examples Arith. & Geo. Seq. Arith. Series Geo. Series
The two simplest sequences to work with are arithmetic and geometric sequences.
An arithmetic sequence goes from one term to the next by always adding (or subtracting) the same value. For instance, 2, 5, 8, 11, 14,... is arithmetic, because each step adds three; and 7, 3, −1, −5,... is arithmetic, because each step subtracts 4 .
The number added (or subtracted) at each stage of an arithmetic sequence is called the "common difference" d , because if you subtract (that is, if you find the difference of) successive terms, you'll always get this common value.
Content Continues Below
MathHelp.com

The number multiplied (or divided) at each stage of a geometric sequence is called the "common ratio" r , because if you divide (that is, if you find the ratio of) successive terms, you'll always get this common value.
Find the common difference and the next term of the following sequence:
3, 11, 19, 27, 35, ...
To find the common difference, I have to subtract a successive pair of terms. It doesn't matter which pair I pick, as long as they're right next to each other. To be thorough, I'll do all the subtractions:
11 − 3 = 8
19 − 11 = 8
27 − 19 = 8
35 − 27 = 8
The difference is always 8 , so the common difference is d = 8 .
They gave me five terms, so the sixth term of the sequence is going to be the very next term. I find the next term by adding the common difference to the fifth term:
35 + 8 = 43
Then my answer is:
common difference: d = 8
sixth term: 43
Find the common ratio and the seventh term of the following sequence:
To find the common ratio, I have to divide a successive pair of terms. It doesn't matter which pair I pick, as long as they're right next to each other. To be thorough, I'll do all the divisions:
The ratio is always 3 , so r = 3 .
They gave me five terms, so the sixth term is the very next term; the seventh will be the term after that. To find the value of the seventh term, I'll multiply the fifth term by the common ratio twice:
a 6 = (18)(3) = 54
a 7 = (54)(3) = 162
common ratio: r = 3
seventh term: 162
Since arithmetic and geometric sequences are so nice and regular, they have formulas.
For arithmetic sequences, the common difference is d , and the first term a 1 is often referred to simply as " a " . Since we get the next term by adding the common difference, the value of a 2 is just:
a 2 = a + d
Continuing, the third term is:
a 3 = ( a + d ) + d = a + 2 d
The fourth term is:
a 4 = ( a + 2 d ) + d = a + 3 d
At each stage, the common difference was multiplied by a value that was one less than the index. Following this pattern, the n -th term a n will have the form:
a n = a + ( n − 1) d
For geometric sequences, the common ratio is r , and the first term a 1 is often referred to simply as " a " . Since we get the next term by multiplying by the common ratio, the value of a 2 is just:
a 3 = r ( ar ) = ar 2
a 4 = r ( ar 2 ) = ar 3
At each stage, the common ratio was raised to a power that was one less than the index. Following this pattern, the n -th term a n will have the form:
a n = ar ( n − 1)
Memorize these n -th-term formulas before the next test.
Find the tenth term and the n -th term of the following sequence:
The first thing I have to do is figure out which type of sequence this is: arithmetic or geometric. I quickly see that the differences don't match; for instance, the difference of the second and first term is 2 − 1 = 1 , but the difference of the third and second terms is 4 − 2 = 2 . So this isn't an arithmetic sequence.
On the other hand, the ratios of successive terms are the same:
2 ÷ 1 = 2
4 ÷ 2 = 2
8 ÷ 4 = 2
(I didn't do the division with the first term, because that involved fractions and I'm lazy. The division would have given the exact same result, though.)
a n = (1/2) 2 n −1 = (2 -1 )(2 n −1 )
=2 (−1) + ( n − 1) = 2 n − 2
To find the value of the tenth term, I can plug n = 10 into the n -th term formula and simplify:
a 10 = 2 10−2 = 2 8 = 256
tenth term: 256
Find the n -th term and the first three terms of the arithmetic sequence having a 6 = 5 and d = katex.render("\\boldsymbol{\\color{green}{\\frac{3}{2}}}", typed07); 3/2
This gives me the first three terms in the sequence. Since I have the value of the first term and the common difference, I can also create the expression for the n -th term, and simplify:
−5/2 + ( n − 1)(3/2)
= −5/2 + (3/2) n − 3/2
= −8/2 + (3/2) n = (3/2) n − 4
Find the n -th term and the first three terms of the arithmetic sequence having a 4 = 93 and a 8 = 65 .
Since a 4 and a 8 are four places apart, then I know from the definition of an arithmetic sequence that I'd get from the fourth term to the eighth term by adding the common difference four times to the fourth term; in other words, the definition tells me that a 8 = a 4 + 4 d . Using this, I can then solve for the common difference d :
65 = 93 + 4 d
−28 = 4 d
−7 = d
Also, I know that the fourth term relates to the first term by the formula a 4 = a + (4 − 1) d , so, using the value I just found for d , I can find the value of the first term a :
93 = a + 3(−7)
93 + 21 = a
Now that I have the value of the first term and the value of the common difference, I can plug-n-chug to find the values of the first three terms and the general form of the n -th term:
a 2 = 114 − 7 = 107
a 3 = 107 − 7 = 100
a n = 114 + ( n − 1)(−7)
= 114 − 7 n + 7 = 121 − 7 n
n -th term: 121 − 7 n
first three terms: 114, 107, 100
Find the n -th and the 26 th terms of the geometric sequence with katex.render("\\boldsymbol{\\color{green}{ \\mathit{a}_5 = \\frac{5}{4} }}", typed16); a 5 = 5/4 and a 12 = 160 .
The two terms for which they've given me numerical values are 12 − 5 = 7 places apart, so, from the definition of a geometric sequence, I know that I'd get from the fifth term to the twelfth term by multiplying the fifth term by the common ratio seven times; that is, a 12 = ( a 5 )( r 7 ) . I can use this to solve for the value of the common ratio r :
160 = (5/4)( r 7 )
Also, I know that the fifth term relates to the first by the formula a 5 = ar 4 , so I can solve for the value of the first term a :
5/4 = a (2 4 ) = 16 a
Now that I have the value of the first term and the value of the common ratio, I can plug each into the formula for the n -th term to get:
a n = (5/64)2 ( n − 1)
= (5/2 6 )(2 n −1 )
= (5)(2 −6 )(2 n −1 )
= 5(2 n −7 )
With this formula, I can evaluate the twenty-sixth term, and simplify:
a 26 = 5(2 19 )
= 2,621,440
26 th term: 2,621,440
Once we know how to work with sequences of arithmetic and geometric terms, we can turn to considerations of adding these sequences.
URL: https://www.purplemath.com/modules/series3.htm
Page 1 Page 2 Page 3 Page 4 Page 5
Standardized Test Prep
College math, homeschool math, share this page.
- Terms of Use
- About Purplemath
- About the Author
- Tutoring from PM
- Advertising
- Linking to PM
- Site licencing
Visit Our Profiles
Unveiling the Power of Algebraic Reasoning

Algebraic reasoning serves as the cornerstone of mathematical problem-solving, providing a systematic approach to understanding relationships, patterns, and structures within numbers and variables. Its significance extends beyond the realms of algebra, influencing critical thinking and problem-solving skills across various disciplines. In this article, we delve into the essence of algebraic reasoning, its indispensable role in mastering algebra, and practical examples of its implementation at different educational levels.
What is Algebraic Reasoning?
At its core, algebraic reasoning involves the ability to identify patterns, generalize relationships, and manipulate symbols to solve problems. It encompasses the use of symbols, variables, and mathematical operations to represent and analyze quantitative relationships. Through algebraic reasoning, students learn to think abstractly, develop logical arguments, and make connections between different mathematical ideas and concepts.
Algebraic reasoning empowers learners to:
- Recognize patterns and regularities in numerical sequences and geometric shapes. - Formulate equations and inequalities to represent real-world situations. - Apply logical reasoning to solve equations and inequalities. - Generalize patterns and relationships to make predictions and solve problems in diverse contexts.
Why is Algebraic Reasoning Essential to Learning Algebra?
Algebra serves as a gateway to advanced mathematical concepts and real-world applications. Mastery of algebraic reasoning lays a solid foundation for navigating the complexities of algebraic expressions, equations, functions, and beyond.
Here's why algebraic reasoning is important in learning algebra:
Abstraction and Symbolism: Algebra introduces students to abstract symbols and variables, requiring them to interpret and manipulate these symbols based on underlying rules and properties. Algebraic reasoning enables learners to understand the symbolic language of algebra and its application in problem-solving. Problem-Solving Skills: Algebraic reasoning fosters analytical thinking and problem-solving skills by encouraging students to break down complex problems into manageable steps, identify relevant information, and devise strategies to reach solutions. It equips students with the tools to tackle a wide range of mathematical challenges with confidence.
Critical Thinking: Algebraic reasoning cultivates critical thinking skills by prompting students to analyze relationships, make conjectures, and justify their conclusions using mathematical evidence. It encourages logical reasoning and the exploration of multiple solution paths, fostering resilience and adaptability in problem-solving. Without these skills, students may struggle to make sense of algebraic concepts and apply them effectively to solve problems. Overall, a lack of proficiency in algebraic reasoning can impede students' progress in algebra and limit their ability to succeed in more advanced mathematical topics and practical applications.
Algebraic Reasoning Examples in Teaching
Elementary school.
Number Patterns: Students explore numerical sequences and identify patterns, such as even or odd numbers, multiples, and sequences of operations (e.g., adding or subtracting a constant). They extend these patterns and predict future terms, laying the groundwork for understanding algebraic patterns. Balancing Equations: Through hands-on activities and visual representations, students learn to balance simple equations using manipulatives or drawings. For example, representing addition and subtraction as inverse operations helps students grasp the concept of equivalence in equations (e.g., 3 + 2 = 5 and 5 - 2 = 3).
Middle School
Variable Expressions: Students learn to translate verbal descriptions into algebraic expressions and vice versa. For instance, they might represent the total cost of items using variables and constants (e.g., \(c = 5p + 3\) where \(c\) represents total cost and \(p\) represents the number of items purchased). Solving Equations: Students solve one-step and two-step equations involving addition, subtraction, multiplication, and division. They apply inverse operations to isolate the variable and determine its value, reinforcing the concept of maintaining balance in equations.
High School
Linear Functions: Students analyze linear relationships between variables and represent them graphically, algebraically, and numerically. They explore concepts such as slope, y-intercept, and rate of change, connecting algebraic representations with real-world scenarios. Systems of Equations: Students solve systems of linear equations using various methods, such as graphing, substitution, and elimination. They apply algebraic reasoning to determine points of intersection and interpret the solutions in context.
Algebraic Reasoning is fundamental to Edmentum Exact Path’s approach to teaching mathematics. By nurturing students' ability to recognize patterns, formulate equations, and solve problems systematically, Exact Path prepares students for Algebra success and equips them with the tools they need to thrive as critical thinkers and problem solvers in an increasingly complex world.
Get the latest education insights sent directly to your inbox
Subscribe to our knowledge articles.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Unit 1: Algebra foundations
Unit 2: solving equations & inequalities, unit 3: working with units, unit 4: linear equations & graphs, unit 5: forms of linear equations, unit 6: systems of equations, unit 7: inequalities (systems & graphs), unit 8: functions, unit 9: sequences, unit 10: absolute value & piecewise functions, unit 11: exponents & radicals, unit 12: exponential growth & decay, unit 13: quadratics: multiplying & factoring, unit 14: quadratic functions & equations, unit 15: irrational numbers, unit 16: creativity in algebra.

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

8.2: Problem Solving with Arithmetic Sequences
- Last updated
- Save as PDF
- Page ID 83159

- Jennifer Freidenreich
- Diablo Valley College
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Arithmetic sequences, introduced in Section 8.1, have many applications in mathematics and everyday life. This section explores those applications.
Example 8.2.1
A water tank develops a leak. Each week, the tank loses \(5\) gallons of water due to the leak. Initially, the tank is full and contains \(1500\) gallons.
- How many gallons are in the tank \(20\) weeks later?
- How many weeks until the tank is half-full?
- How many weeks until the tank is empty?
This problem can be viewed as either a linear function or as an arithmetic sequence. The table of values give us a few clues towards a formula.

The problem allows us to begin the sequence at whatever \(n\)−value we wish. It’s most convenient to begin at \(n = 0\) and set \(a_0 = 1500\).
Therefore, \(a_n = −5n + 1500\)
Since the leak is first noticed in week one, \(20\) weeks after the initial week corresponds with \(n = 20\). Use the formula where \(\textcolor{red}{n = 20}\):
\(a_{20} = −5(\textcolor{red}{20}) + 1500 = −100 + 1500 = 1400\)
Therefore, \(20\) weeks later, the tank contains \(1400\) gallons of water.
- How many weeks until the tank is half-full? A half-full tank would be \(750\) gallons. We need to find \(n\) when \(\textcolor{red}{a_n = 750}\).
\(\begin{array} &750 &= −5n + 1500 &\text{Substitute \(a_n = 750\) into the general term.} \\ 750 − 1500 &= −5n + 1505 − 1500 &\text{Subtract \(1500\) from each side of the equation.} \\ −750 &= −5n &\text{Simplify each side of the equation.} \\ \dfrac{−750}{−5} &= \dfrac{−5n}{−5} &\text{Divide both sides by \(−5\).} \\ 150 &= n & \end{array}\)
Since \(n\) is the week-number, this answer tells us that on week \(150\), the tank is half full. However, most people would better understand the answer if stated in the following way, “The tank is half full after 150 weeks.” This answer sounds more natural and is preferred.
- How many weeks until the tank is empty? The tank is empty when \(a_n = 0\) gallons. Find \(n\) such that \(\textcolor{red}{a_n = 0}\).
\(\begin{array}& 0 &= −5n + 1500 &\text{Substitute \(a_n=0\) into the general term.} \\ 0 − 1500 &= −5n + 1500 − 1500 &\text{Subtract \(1500\) from each side of the equation.} \\ −1500 &= −5n &\text{Simplify.} \\ \dfrac{−1500}{−5} &= \dfrac{−5n}{−5} &\text{Divide both sides by \(−5\).} \\ 300 &= n & \end{array}\)
Since \(n\) is the week-number, this answer tells us that on week \(300\), the tank is empty. However, most people would better understand the answer if stated in the following way, “ The tank is empty after 300 weeks. ” This answer sounds more natural and is preferred.
Example 8.2.2
Three stages of a pattern are shown below, using matchsticks. Each stage requires a certain number of matchsticks. If we keep up the pattern…
- How many matchsticks are required to make the figure in stage \(34\)?
- What stage would require \(220\) matchsticks?
| Stage 1 | Stage 2 | Stage 3 |
Let’s create a table of values. Let \(n =\) stage number, and let \(a_n =\) the number of matchsticks used in that stage. Then note the common difference.
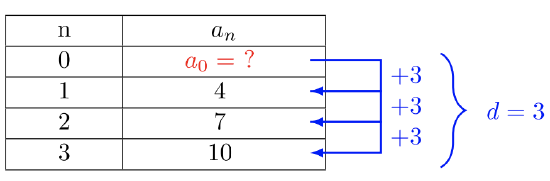
Find the value \(a_0\):
\(\begin{array} &a_0 + 3 &= 4 \\ a_0 + 3 − 3 &= 4 − 3 \\ a_0 &= 1 \end{array}\)
The general term of the sequence is:
\(a_n = 3n + 1\)
- Compute \(a_{34}\) to find the number of matchsticks in stage \(34\):
\(a_{34} = 3(\textcolor{red}{34}) + 1 = 103\).
There are \(103\) matchsticks in stage \(34\).
- What stage would require \(220\) matchsticks? We are looking for the stage-number, given the number of matchsticks. Find \(n\) if \(a_n = 220\).
\(\begin{array} &220 &= 3n + 1 \\ 219 &= 3n \\ 73 &= n \end{array}\)
Answer Stage \(73\) would require \(220\) matchsticks.
Example 8.2.3
Cory buys \(5\) items at the grocery store with prices \(a_1\), \(a_2\), \(a_3\), \(a_4\), \(a_5\) which is an arithmetic sequence. The least expensive item is \($1.89\), while the total cost of the \(5\) items is \($12.95\). What is the cost of each item?
Put the \(5\) items in order of expense: least to most and left to right. Because it is an arithmetic sequence, each item is \(d\) more dollars than the previous item. Each item’s price can be written in terms of the price of the least expensive item, \(a_1\), and \(a_1 = $1.89\).
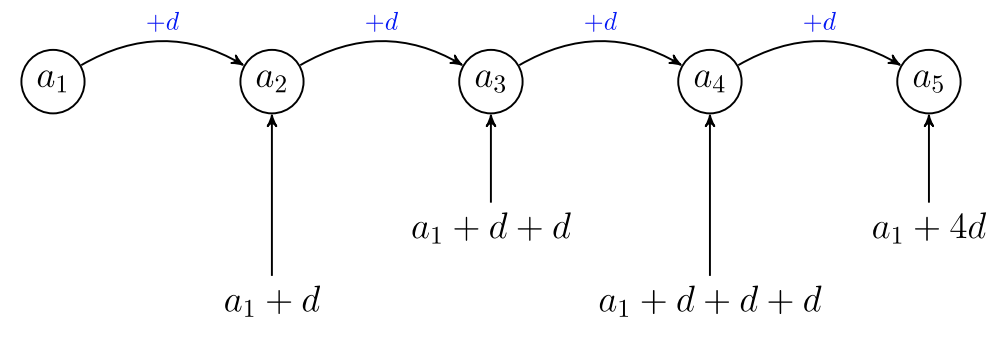
The diagram above gives \(5\) expressions for the costs of the \(5\) items in terms of \(a_1\) and the common difference is \(d\).
\(\begin{array} &a_1 + a_2 + a_3 + a_4 + a_5 &= 12.95 &\text{Total cost of \(5\) items is \($12.95\).} \\ a_1 + (a_1 + d) + (a_1 + 2d) + (a_1 + 3d) + (a_1 + 4d) &= 12.95 &\text{See diagram for substitutions.} \\ 5s_1 + 10d &= 12.95 &\text{Gather like terms.} \\ 5(1.89) + 10d &= 12.95 &a_1 = 1.89. \\ 9.45 + 10d &= 12.95 &\text{Simplify.} \\ 9.45 + 10d − 9.45 &= 12.95 − 9.45 &\text{Subtract \(9.45\) from each side of equation.} \\ 10d &= 3.50 &\text{Simplify. Then divide both sides by \(10\).} \\ d &= 0.35 &\text{The common difference is \($0.35\).} \end{array}\)
Now that we know the common difference, \(d = $0.35\), we can answer the question.

The price of each item is as follows: \($1.89, $2.24, $2.59, $2.94, $3.29\).
Try It! (Exercises)
1. ZKonnect cable company requires customers sign a \(2\)-year contract to use their services. The following describes the penalty for breaking contract: Your services are subject to a minimum term agreement of \(24\) months. If the contract is terminated before the end of the \(24\)-month contract, an early termination fee is assessed in the following manner: \($230\) termination fee is assessed if contract is terminated in the first \(30\) days of service. Thereafter, the termination fee decreases by \($10\) per month of contract.
- If Jack enters contract with ZKonnect on April 1 st of \(2021\), but terminates the service on January 10 th of \(2022\), what are Jack’s early termination fees?
- The general term \(a_n\) describes the termination fees for the stated contract. Describe the meaning of the variable \(n\) in the context of this problem. Find the general term \(a_n\).
- Is the early termination fee a finite sequence or an infinite sequence? Explain.
- Find the value of \(a_{13}\) and interpret its meaning in words.
2. A drug company has manufactured \(4\) million doses of a vaccine to date. They promise additional production at a rate of \(1.2\) million doses/month over the next year.
- How many doses of the vaccine, in total, will have been produced after a year?
- The general term \(a_n\) describes the total number of doses of the vaccine produced. Describe the meaning of the variable \(n\) in the context of this problem. Find the general term\(a_n\).
- Find the value of \(a_8\) and interpret its meaning in words.
3. The theater shown at right has \(22\) seats in the first row of the “A Center” section. Each row behind the first row gains two additional seats.
- Let \(a_n = 22 + 2n\), starting with \(n = 0\). Give the first \(10\) values of this sequence.
- Using \(a_n = 22 + 2n\), Find the value of \(a_{10}\) and interpret its meaning in words in the context of this problem. Careful! Does \(n=\) row number?
- How many seats, in total, are in “A Center” section if there are \(12\) rows in the section?
4) Logs are stacked in a pile with \(48\) logs on the bottom row and \(24\) on the top row. Each row decreases by three logs.
- The stack, as described, has how many rows of logs?
- Write the general term \(a_n\) to describe the number of logs in a row in two different ways. Each general term should produce the same sequence, regardless of its starting \(n\)-value.
i. Start with \(n = 0\).
ii. Start with \(n = 1\).
5) The radii of the target circle are an arithmetic sequence. If the area of the innermost circle is \(\pi \text{un}^2\) and the area of the entire target is \(49 \pi \text{un}^2\), what is the area of the blue ring? [The formula for area of a circle is \(A = \pi r^2\)].
6) Three stages of a pattern are shown below, using matchsticks. Each stage adds another triangle and requires a certain number of matchsticks. If we keep up the pattern…
- What stage would require \(325\) matchsticks?
7) Three stages of a pattern are shown below, using matchsticks. Each stage requires a certain number of matchsticks. If we keep up the pattern…
- How many matchsticks are required to make the figure in stage \(22\)?
- What stage would require \(424\) matchsticks?

IMAGES
VIDEO
COMMENTS
Geometric sequences are sequences in which the next number in the sequence is found by multiplying the previous term by a number called the common ratio. The common ratio is denoted by the letter r. Depending on the common ratio, the geometric sequence can be increasing or decreasing. If the common ratio is greater than 1, the sequence is ...
Problems with Solutions. Find the terms a 2, a 3, a 4 and a 5 of a geometric sequence if a 1 = 10 and the common ratio r = - 1. Find the 10 th term of a geometric sequence if a 1 = 45 and the common ration r = 0.2. Solution to Problem 2: Use the formula. Find a 20 of a geometric sequence if the first few terms of the sequence are given by.
Example 1: continuing a geometric sequence. Calculate the next three terms for the geometric progression 1, 2, 4, 8, 16, 1, 2,4,8,16, …. Take two consecutive terms from the sequence. Here we will take the numbers 4 4 and 8 8. 2 Divide the second term by the first term to find the value of the common ratio, r r.
Geometric sequence formulas give a ( n) , the n th term of the sequence. This is the explicit formula for the geometric sequence whose first term is k and common ratio is r : a ( n) = k ⋅ r n − 1. This is the recursive formula of that sequence: { a ( 1) = k a ( n) = a ( n − 1) ⋅ r.
Sharpen your math proficiency with these Geometric Series Practice Problems. Solve ten (10) questions and verify your solutions by comparing them with the provided answers. ... Geometric Series Practice Problems with Answers. ... here's the geometric series formula: Problem 1: Find the sum of the first nine (9) terms of the geometric series ...
Example: Sum the first 4 terms of 10, 30, 90, 270, 810, 2430, ... This sequence has a factor of 3 between each number. ... So our infnite geometric series has a finite sum when the ratio is less than 1 (and greater than −1) Let's bring back our previous example, and see what happens:
The sequence below is an example of a geometric sequence because each term increases by a constant factor of 6. Multiplying any term of the sequence by the common ratio 6 generates the subsequent term. ... Solving Application Problems with Geometric Sequences. In 2013, the number of students in a small school is \(284\). It is estimated that ...
Definition 12.4.4. An infinite geometric series is an infinite sum whose first term is a1 and common ratio is r and is written. a1 + a1r + a1r2 + … + a1rn − 1 + …. We know how to find the sum of the first n terms of a geometric series using the formula, Sn = a1(1 − rn) 1 − r.
The sequence below is an example of a geometric sequence because each term increases by a constant factor of 6. Multiplying any term of the sequence by the common ratio 6 generates the subsequent term. ... Solving Application Problems with Geometric Sequences. In 2013, the number of students in a small school is 284. It is estimated that the ...
Find the Sum of the First n Terms of a Geometric Sequence. We found the sum of both general sequences and arithmetic sequence. We will now do the same for geometric sequences. The sum, S n, of the first n terms of a geometric sequence is written as S n = a 1 + a 2 + a 3 + ... + a n. We can write this sum by starting with the first term, a 1 ...
Solve Word Problems using Geometric Sequences. Example: Wilma bought a house for $170,000. Each year, it increases 2% of its value. ... Show Video Lesson. Application of a Geometric Sequence. Example: Bouncing ball application of a geometric sequence When a ball is dropped onto a flat floor, it bounces to 65% of the height from which it was ...
A series, the most conventional use of the word series, means a sum of a sequence. So for example, this is a geometric sequence. A geometric series would be 90 plus negative 30, plus 10, plus negative 10/3, plus 10/9. ... But anyway, let's go back to the notion of a geometric sequence, and actually do a word problem that deals with one of these ...
In algebra, a geometric sequence, sometimes called a geometric progression, is a sequence of numbers such that the ratio between any two consecutive terms is constant. This constant is called the common ratio of the sequence. For example, is a geometric sequence with common ratio and is a geometric sequence with common ratio ; however, and are ...
Exercise 9.3.3. Find the sum of the infinite geometric series: ∑∞ n = 1 − 2(5 9)n − 1. Answer. A repeating decimal can be written as an infinite geometric series whose common ratio is a power of 1 / 10. Therefore, the formula for a convergent geometric series can be used to convert a repeating decimal into a fraction.
How to Solve Infinite Geometric Series; How to Solve Arithmetic Sequences; Step by step guide to solve Geometric Sequence Problems. It is a sequence of numbers where each term after the first is found by multiplying the previous item by the common ratio, a fixed, non-zero number. For example, the sequence \(2, 4, 8, 16, 32\), … is a geometric ...
The first term and the common ratio are both given in the problem. The only thing we have to do is to plug these values into the geometric sequence formula then use it to find the nth term of the sequence. a)The first term is [latex]\large{{a_1} = 3}[/latex] while its common ratio is [latex]r = 2[/latex]. This gives us.
Many real-world problems involve geometric sequences and series. The following definitions can help us solve these problems. A finite geometric sequence has the form 𝑇, 𝑇 𝑟, 𝑇 𝑟, …, 𝑇 𝑟 , where 𝑇 is the first term, 𝑟 is the common ratio, and 𝑛 is the number of terms in the sequence.
Explicit formulas for geometric sequences. Wang Lei and Amira were asked to find an explicit formula for the sequence 30, 150, 750, 3750, … , where the first term should be g ( 1) . Wang Lei said the formula is g ( n) = 30 ⋅ 5 n − 1 , and. Amira said the formula is g ( n) = 6 ⋅ 5 n .
Example #2: The third term of a geometric sequence is 45 and the fifth term of the geometric sequence is 405. If all the terms of the sequence are positive numbers, find the 15th term of the geometric sequence. Solution To solve this problem, we need the geometric sequence formula shown below. a n = a 1 × r (n - 1) Find the third term
an = a + ( n − 1) d. For geometric sequences, the common ratio is r, and the first term a1 is often referred to simply as "a". Since we get the next term by multiplying by the common ratio, the value of a2 is just: a2 = ar. Continuing, the third term is: a3 = r ( ar) = ar2. The fourth term is: a4 = r ( ar2) = ar3.
Solution. Finding the common ratio is a matter of dividing any term by its previous term: 45 15 = 3 = r 45 15 = 3 = r. Therefore, the general term of the sequence is: an = 15 ⋅3n−1 a n = 15 ⋅ 3 n − 1. The general term gives us a formula to find a10 a 10. Plug n = 10 n = 10 into the general term an a n.
The sequence below is an example of a geometric sequence because each term increases by a constant factor of 6. Multiplying any term of the sequence by the common ratio 6 generates the subsequent term. ... Solving Application Problems with Geometric Sequences. In 2013, the number of students in a small school is 284. It is estimated that the ...
- Recognize patterns and regularities in numerical sequences and geometric shapes. - Formulate equations and inequalities to represent real-world situations. - Apply logical reasoning to solve equations and inequalities. - Generalize patterns and relationships to make predictions and solve problems in diverse contexts.
The Algebra 1 course, often taught in the 9th grade, covers Linear equations, inequalities, functions, and graphs; Systems of equations and inequalities; Extension of the concept of a function; Exponential models; and Quadratic equations, functions, and graphs. Khan Academy's Algebra 1 course is built to deliver a comprehensive, illuminating, engaging, and Common Core aligned experience!
Solution. This problem can be viewed as either a linear function or as an arithmetic sequence. The table of values give us a few clues towards a formula. The problem allows us to begin the sequence at whatever n n −value we wish. It's most convenient to begin at n = 0 n = 0 and set a0 = 1500 a 0 = 1500.