assignment 17 1 verifying solutions for linear inequalities

Solving Linear Inequalities Worksheets with Solutions

Solving linear inequalities is a foundational skill that you will build throughout your studies of elementary and high school algebra. While it isn’t the hardest concept you will encounter in the entire class, there are a few tips and tricks you should get used to. And the best way to do that is by practicing! 

That’s why I put together this collection of solving linear inequalities worksheets! Let’s dig in so that you can master this important algebra concept!

What is a Linear Inequality?

A linear inequality is a type of statement in algebra that compares two linear equations. To make this comparison, we place an inequality symbol in between the two sides of the inequality. For example, \(x+1>2x-1\).

Take a moment to review this inequality symbol list:

• < (less than)
• > (greater than)
• ≤ (less than or equal to)
• ≥ (greater than or equal to)

Linear inequalities are similar to linear equations, however instead of an equals sign, a linear inequality contains one of the inequality symbols from the above list.

How to Solve a Linear Inequality

The steps that you take to solve a linear inequality are a very similar to those that you would take while  solving an algebraic equation . When solving linear inequalities, you often perform similar operations as you would when  solving linear equations . 

Just like in linear equations, you can add or subtract terms on both sides, and multiply or divide by constants on both sides. However, unlike solving linear equations, linear inequalities have one  very  important rule:

Remember: If you multiply or divide both sides of an inequality by a negative number, the inequality sign must be flipped! 

You will see some examples of this in the solving linear inequalities worksheets linked below!

Another important difference between solving a linear equation and solving a linear inequality is that the solution to a linear inequality will be the  set of all values  that make the inequality true (rather than just a  single value  that makes the equation true).

The solution to a linear inequality will tell you the places on the graph where one line is greater than or less than the other.

For example, consider the coordinate plane below that shows two lines in slope-intercept form. 

As you can see, the red line is above the green line as long as \(x<2\). After this, the green line is above the red line. So if we wanted to write the solution to \(x+1>2x-1\), we would say that the solution set is \(x<2\), or all x-values less than 2 (note that we do not include 2 in the solution set since that is the point where the lines are equal ).

Solving Algebraically

In order to solve \(x+1>2x-1\) algebraically, we will use the same algebra strategies that we use when solving linear equations. We will collect all x-terms on the left side of the equation, and all non-variable terms on the right side of the equation.

\begin{split} x+1&>2x-1 \\ \\ -x&>-2 \\ \\ x&<2 \end{split}

Since we had to divide both sides by -1, notice that we flipped the sign of the inequality symbol! Therefore, the solution to this inequality is x<2 (which we can confirm using the coordinate plane above).

Another way that we can represent this solution is on a number line . We draw a line to the left of 2 with a hollow circle at 2 to indicate that 2 is  not  part of our solution set. We would use a filled in dot to indicate a value that  is  part of the solution set.

There are many ways to solve linear inequalities and represent their solutions. In the math worksheets that follow below, you will focus mainly on solving algebraically and representing your answer on a number line!

One-Step Inequalities Math Worksheet

To get started, try the set of one-step inequalities in the worksheet linked below. These problems will help you become familiar with solving a linear equality algebraically, and representing the solution on a number line. 

I have created this worksheet in PDF format for your convenience. Remember to check the answer key provided to make sure that you understand the basics of solving linear inequalities.

Download the PDF worksheet by clicking below!

Multi-Step Inequalities Math Worksheet

Now that you have had some practice with solving one-step inequality problems, use the following worksheet to try your hand at some more complex linear inequality problems. This worksheet contains two-step inequalities as well as some more difficult multi-step linear inequality problems! 

This worksheet is also provided in PDF format for ease of access. Remember to check the answer key to confirm your understanding of solving more complex linear inequalities.

Practice Solving Linear Inequalities

Inequalities may seem scary at first because of the inequality symbol, but as you have seen, they are actually solved in a very similar way to linear equations.

Use the math worksheets linked above to practice getting comfortable with solving a variety of linear inequality problems. Like any math concept, the more you practice the more familiar the concept will start to feel.

I hope these solving linear inequalities worksheets have helped you practice your inequality solving skills, as well as representing the solution set on a number line!

Ready to start applying your skills? Check out this linear inequalities word problems worksheet !

Did you find these solving linear inequalities worksheets helpful? Share this post and subscribe to Math By The Pixel on YouTube for more helpful mathematics content!

RECOMMENDED FOR YOU

Quadratic Formula Word Problems Answer Key and Lesson

4 All Students Take Calculus Examples for Trigonometry

5.3 Linear Inequalities in One Variable with Applications

Learning objectives.

After completing this section, you should be able to:

• Graph inequalities in one variable.
• Solve linear inequalities in one variable.
• Construct a linear inequality to solve applications.

In this section, we will study linear inequalities in one variable. Inequalities can be used when the possible values (answers) in a certain situation are numerous, not just a few, or when the exact value (answer) is not known but it is known to be within a range of possible values. There are many real-world scenarios that can be represented by linear inequalities. For example, consider the survey of the mayoral election in Figure 5.5 Surveys and polls are usually conducted with only a small group of people. The margin of error indicates a range of how the actual group of voters would vote given the results of the survey. This range can be expressed using inequalities.

Another example involves college tuition. Say a local community college charges $113 per credit hour. You budget $1,500 for tuition this fall semester. What are the number of credit hours that you could take this fall? Since this answer could be many different values, it can be expressed as an inequality.

Graphing Inequalities on the Number Line

In Algebraic Expressions , we introduced equality and the = = symbol. In this section, we look at inequality and the symbols < < , > > , ≤ ≤ , and ≥ ≥ . The table below summarizes the symbols and their meaning.

Suppose you had the inequality statement x > 3 x > 3 . What possible number or numbers would make the inequality x > 3 x > 3 true? If you are thinking, " x x could be 4," that's correct, but x x could also be 5, 6, 37, 1 million, or even 3.001. The number of solutions is infinite; any number greater than 3 is a solution to the inequality x > 3 x > 3 .

Rather than trying to list all possible solutions, we show all the solutions to the inequality x > 3 x > 3 on the number line. All the numbers to the right of 3 on the number line are shaded, to show that all numbers greater than 3 are solutions. At the number 3 itself, an open parenthesis is drawn, since the number 3 is not part of the solutions of x > 3 x > 3 .

We can also represent inequalities using interval notation. There is no upper end to the solution to this inequality. In interval notation, we express x > 3 x > 3 as ( 3 , ∞ ) ( 3 , ∞ ) . The symbol ∞ ∞ is read as "infinity." Infinity is not an actual number. Figure 5.6 shows both the number line and the interval notation for x > 3 x > 3 .

We used the left parenthesis symbol to show that the endpoint of the inequality is not included. Parentheses are used when the endpoints are not included as a possible answer to the inequality. The notation for inequalities on a number line and in interval notation use the same symbols to express the endpoints of intervals.

The inequality x ≤ 1 x ≤ 1 means all numbers less than or equal to 1. To illustrate that solution on a number line, we first put a bracket at x = 1 x = 1 ; brackets are used when the endpoint is included. We then shade in all the numbers to the left of 1, to show that all numbers less than one are solutions. There is no lower end to those numbers. We write x ≤ 1 x ≤ 1 in interval notation as ( − ∞ , 1 ] ( − ∞ , 1 ] . The symbol − ∞ − ∞ is read as "negative infinity." Figure 5.7 shows both the number line and interval notation for x = 1 x = 1 .

Figure 5.8 summarizes the general representations in both number line form and interval notation of solutions for x > a x > a , x < a x < a , x ≥ a x ≥ a , and x ≤ a x ≤ a .

Example 5.21

Graphing an inequality.

Graph the inequality x ≥ − 3 x ≥ − 3 and write the solution in interval notation.

Shade to the right of − 3 − 3 to show all the numbers greater than − 3 − 3 , and put a bracket at − 3 − 3 to show that the numbers are greater than or equal to − 3 − 3 ( Figure 5.9 )

Write in interval notation starting at − 3 − 3 with a bracket to show that − 3 − 3 is included in the solution and then infinity because the solution includes all the numbers greater than or equal to − 3 − 3 :

Your Turn 5.21

Example 5.22, graphing a compound inequality.

Graph the inequality x > − 3 x > − 3 and x < 4 x < 4 and write the solution in interval notation.

Step 1: Graph x > − 3 x > − 3 ( Figure 5.10 ).

Step 2: Graph x < 4 x < 4 ( Figure 5.11 ).

Step 3: Graph both on the same number line and think of where the solutions are to BOTH inequalities Figure 5.12 . This will be where BOTH are shaded.

Step 4: Write the solution in interval notation:

Your Turn 5.22

Where did the inequality symbols come from.

The first use of the < < symbol to represent "less than" and > > to represent "greater than" appeared in a mathematics book written by Englishman Thomas Harriot that was published in 1631. However, Harriot did not invent the symbols…the editor of the book did! Harriot used triangular symbols to represent less than and greater than; the editor, for reasons unknown, changed to symbols that are similar to the ones we use today. The symbols used to represent less than or equal to, and greater than or equal to ( ≤ ≤ and ≥ ≥ ) were first used in 1731 by French hydrologist and surveyor Pierre Bouguer. Interestingly, English mathematician John Wallis had used similar symbols as early as 1670, but he put the bar above the less than and greater than symbols instead of below them.

Solving Linear Inequalities

A linear inequality is much like a linear equation—but the equal sign is replaced with an inequality sign. A linear inequality is an inequality in one variable that can be written in one of the forms a x + b < c , a x + b ≤ c , a x + b ≥ c , a x + b < c , a x + b ≤ c , a x + b ≥ c , or a x + b > c , a x + b > c , where a a , b b , and c c are all real numbers.

When we solved linear equations, we were able to use the properties of equality to add, subtract, multiply, or divide both sides and still keep the equality. Similar properties hold true for inequalities. We can add or subtract the same quantity from both sides of an inequality and still keep the inequality. For example, we know that 2 is less than 4, i.e., 2 < 4 2 < 4 . If we add 6 to both sides of this inequality, we still have a true statement:

The same would happen if we subtracted 6 from both sides of the inequality; the statement would stay true:

Notice that the inequality signs stayed the same. This leads us to the Addition and Subtraction Properties of Inequality.

For any numbers a a , b b , and c c , if a < b a < b , then a + c < b + c a + c < b + c and a − c < b − c a − c < b − c .

For any numbers a a , b b , and c c , if a > b a > b , then a + c > b + c a + c > b + c and a - c > b - c a - c > b - c .

We can add or subtract the same quantity from both sides of an inequality and still keep the inequality the same. But what happens to an inequality when we divide or multiply both sides by a number? Let's first multiply and divide both sides by a positive number, starting with an inequality we know is true, 10 < 15 10 < 15 . We will multiply and divide this inequality by 5:

The inequality signs stayed the same. Does the inequality stay the same when we divide or multiply by a negative number? Let's use our inequality 10 < 15 10 < 15 to find out, multiplying it and dividing it by − 5 − 5 :

Notice that when we filled in the inequality signs, the inequality signs reversed their direction in order to make it true! To summarize, when we divide or multiply an inequality by a positive number, the inequality sign stays the same. When we divide or multiply an inequality by a negative number, the inequality sign reverses. This gives us the Multiplication and Division Property of Inequality.

For any numbers a a , b b , and c c ,

To summarize, when we divide or multiply an inequality by:

• a positive number, the inequality sign stays the same.
• a negative number, the inequality sign reverses.

Be careful to only reverse the inequality sign when you are multiplying and dividing by a negative. You do NOT reverse the inequality sign when you add or subtract a negative. For example, 2 x < − 4 2 x < − 4 is solved by dividing both sides of the inequality by 2 to get x < − 2 x < − 2 . You do NOT reverse the inequality sign because there is a negative 4. As another example, − 2 x + 5 < 3 x − 2 x + 5 < 3 x is solved by adding − 2 x − 2 x to both sides to get 5 < 5 x 5 < 5 x . This does not reverse the inequality sign because we were not multiplying or dividing by a negative. We then divide both sides by 5 and get 1 < x 1 < x .

Example 5.23

Solving a linear inequality using one operation.

Solve 9 y < 54 9 y < 54 , graph the solution on the number line, and write the solution in interval notation.

9 y < 54 9 y 9 < 54 9 y < 6 9 y < 54 9 y 9 < 54 9 y < 6

Your Turn 5.23

Example 5.24, solving a linear inequality using multiple operations.

Solve the inequality 6 y ≤ 11 y + 17 6 y ≤ 11 y + 17 , graph the solution on the number line, and write the solution in interval notation.

Your Turn 5.24

Solving applications with linear inequalities.

Many real-life situations require us to solve inequalities. The method we will use to solve applications with linear inequalities is very much like the one we used when we solved applications with equations. We will read the problem and make sure all the words are understood. Next, we will identify what we are looking for and assign a variable to represent it. We will restate the problem in one sentence to make it easy to translate into an inequality. Then, we will solve the inequality.

Sometimes an application requires the solution to be a whole number, but the algebraic solution to the inequality is not a whole number. In that case, we must round the algebraic solution to a whole number. The context of the application will determine whether we round up or down.

Example 5.25

Constructing a linear inequality to solve an application with tablet computers.

A teacher won a mini grant of $4,000 to buy tablet computers for their classroom. The tablets they would like to buy cost $254.12 each, including tax and delivery. What is the maximum number of tablets the teacher can buy?

Let t = the number of tablets . t = the number of tablets .

t t times $254.12 has to be less than $4,000, so 254.12 t ≤ 4 , 000 254.12 t ≤ 4 , 000 .

Solve for t t :

The teacher can buy 15 tablets and stay under $4,000.

Your Turn 5.25

Example 5.26, constructing a linear inequality to solve a tuition application.

The local community college charges $113 per credit hour. Your budget is $1,500 for tuition this fall semester. What number of credit hours could you take this fall?

Let c = c = the number of credit hours you could take.

c c times $113 has to be less than $1,500, so 113 c ≤ 1 , 500 113 c ≤ 1 , 500 .

Solve for c c :

You can take up to 13 credits and stay under $1,500.

Your Turn 5.26

Example 5.27, constructing a linear inequality to solve an application with travel costs.

Brenda’s best friend is having a destination wedding and the event will last 3 days and 3 nights. Brenda has $500 in savings and can earn $15 an hour babysitting. She expects to pay $350 for airfare, $375 for food and entertainment, and $60 a night for her share of a hotel room. How many hours must she babysit to have enough money to pay for the trip?

Let b = b = number of babysitting hours.

b b times $15 plus $500 has to be more than $ 350 + $ 375 + $ 60 / night $ 350 + $ 375 + $ 60 / night , so 15 b + 500 ≥ 350 + 375 + 60 ( 3 ) 15 b + 500 ≥ 350 + 375 + 60 ( 3 ) .

Solve for b b :

Brenda must babysit at least 27 hours.

Your Turn 5.27

The Desmos activities called "Inequalities on a Number Line" and "Compound Inequalities on a Number Line" are ways for students to develop and deepen their understanding of inequalities. Teachers will need a Desmos account to assign the activity for student use. Once they have assigned the activity to their students, teachers need to share the code for the activity with their students. Students will input the code to work on the activity.

Check Your Understanding

• [ − 1 , ∞ )
• ( − 1 , 1 )
• ( − ∞ , 1 )
• ( − ∞ , − 1 )
• ( − 5 , ∞ )
• [ − 5 , ∞ )
• [ − 5 , − 3 )
• [ − 5 , − 3 ]
• [ 3 2 , ∞ )
• ( 3 2 , ∞ )
• ( ∞ , 3 2 )
• ( − 4 , 3 )
• ( 3 , − 4 )
• [ − ∞ , ∞ )
• [ − 4 , 3 ]
• [ 3 , − 4 ]
• 6 x < 24
• 24"> 6 x > 24
• − 6 x < 18
• 18"> − 6 x > 18
• − 6 x ≤ − 18
• - 8"> − 4 x > − 8
• - 11"> 4 x + 3 > − 11
• - 11"> 4 x − 3 > − 11
• − 4 x ≤ − 8
• − 4 x + 3 ≤ 5
• - 13"> − 3 x + 14 > − 13
• - 13"> − 3 x − 14 > − 13
• 8 < 764 x
• 8 x < 764
• 764x"> 8 > 764 x
• 764"> 8 x > 764
• None of these
• 50 < 8,120x
• 50 x < 8,120
• \text{8,120}"> 50 x > 8,120

Section 5.3 Exercises

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction

• Authors: Donna Kirk
• Publisher/website: OpenStax
• Book title: Contemporary Mathematics
• Publication date: Mar 22, 2023
• Location: Houston, Texas
• Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
• Section URL: https://openstax.org/books/contemporary-mathematics/pages/5-3-linear-inequalities-in-one-variable-with-applications

© Jul 25, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• Solutions Integral Calculator Derivative Calculator Algebra Calculator Matrix Calculator More...
• Graphing Line Graph Exponential Graph Quadratic Graph Sine Graph More...
• Calculators BMI Calculator Compound Interest Calculator Percentage Calculator Acceleration Calculator More...
• Geometry Pythagorean Theorem Calculator Circle Area Calculator Isosceles Triangle Calculator Triangles Calculator More...
• Tools Notebook Groups Cheat Sheets Worksheets Study Guides Practice Verify Solution

Study Guides > MATH 0123

Graph solutions to systems of linear inequalities, learning outcomes.

• Solve systems of linear inequalities by graphing the solution region
• Graph solutions to a system that contains a compound inequality

Licenses & Attributions

Cc licensed content, original.

• Ex 1: Graph a System of Linear Inequalities. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution .

CC licensed content, Shared previously

• Ex 2: Graph a System of Linear Inequalities. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution .
• Determine the Solution to a System of Inequalities (Compound). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution .
• Unit 14: Systems of Equations and Inequalities, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology Located at: https://www.nroc.org/. License: CC BY: Attribution .

We want your feedback

Please add a message.

Message received. Thanks for the feedback.

Linear Inequalities in Two Variables

In this mini-lesson, we will learn about infinite sets, ordered pairs, graph linear inequalities in two variables, greater than or equal to, less than or equal to, linear inequalities in two variables and graphing two variable inequalities.

But here's an interesting bit of trivia: Did you know that Thomas Harriot was the person who introduced the concept of inequalities in his book "Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas" in 1631.

Lesson Plan

What are linear inequalities in two variables.

When one expression is given to be greater than or less than another expression, we have an inequality .

Linear inequalities are defined as expressions where two values are compared using inequality symb ols.   The s ymbols representing inequalities are:

Not equal (\(\neq\)) Less than (\(<\)) Greater than  (\(>\)) Less than or equal to (\(\leq\)) Greater than or equal to  (\(\geq\))

Linear inequalities in two variables represent the inequal relationship between two algebraic expressions which includes two distinct variables .

A  linear inequality in two variables  is formed when symbols other than equal to, such as greater than or less than are used to relate two expressions, and two variables are involved.

Here are some examples of linear inequalities in two variables:

\[\begin{array}{l}2x< 3y + 2\\7x - 2y > 8\\3x + 4y + 3 \le 2y - 5\\y + x \ge 0\end{array}\]

How Do You Solve Linear Inequalities With Two Variables?

The solution of a linear inequality in two variables, like Ax + By > C, is an ordered pair (x, y) that produces a true statement when the values of x and y are substituted into the inequality.

Solving linear inequalities is the same as solving linear equations; the difference it holds is of inequality symbol.

We solve linear inequalities in the same way as linear equations.

Step 1: Simplify the inequality on both sides, on LHS as well as RHS as per the rules of inequality.  Step 2: Once the value is obtained, we have:

• strict inequalities, in which the two sides of the inequalities cannot be equal to each other.
• non-strict inequalities, in which the two sides of the inequalities can also be equal.

Consider the following inequality:

\[2x +3y > 7\]

When we talk about finding the solution to this inequality , we are talking about all those pairs of values  of x and y for which this inequality is satisfied. This means, for example, that \(x = 4,\;y = 3\) is one possible solution to this particular inequality. However, \(x = 0,\;y = 0\) is not, because when you substitute x and y equal to 0 on the LHS of the inequality, it turns out to be less than 7.

We saw that for any linear equation in two variables, there are infinitely many solutions. It might be obvious to you now that for any linear inequality as well, we will have infinitely many solutions. All these solutions will constitute the solution set of the linear inequality. 

• PEMDAS and BODMAS play a crucial role in solving inequalities.
• If the number is negative on either side of a sign (not both), the direction stays the same.

How Do you Graph Inequalities With Two Variables?

Linear inequalities in two variables have infinite sets or infinitely many ordered pair solutions.

These ordered pairs or the solution sets can be graphed in the appropriate half of a rectangular coordinate plane.

In order to graph inequalities with two variables,

• Identify the type of inequality (greater than, less than, greater than or equal to, less than or equal to).
• Graph the boundary line - a dashed (in case of strict inequality) or a solid line (in case of non-strict inequalities).
• Choose a test point, most probably (0,0) or any other point which is not on the boundary.
• Shade the region accordingly. If the test point solves the inequality, shade the region that contains it. Otherwise, shade the opposite side of the boundary line.
• Verify with more number of test points in and out of the region.

Example: Graph the linear equality \[2x + 3y > 7\]

• Plot the straight line corresponding to the linear equation \(2x + 3y = 7\).
• Determine any two points (solutions) for this equation:  two possible points on the graph can be taken as \(A\left( { - 1,\;3}\right),\,\,B\left( {2,\;1} \right)\) and plot them on the graph.
• Determine some specific solutions for the linear inequality \[2x + 3y > 7\], which can be as follows \begin{equation}(2,3), (3,1), (4.5,0), (0,3), (1.5,2)\end{equation}
• Plot these five points on the same graph.

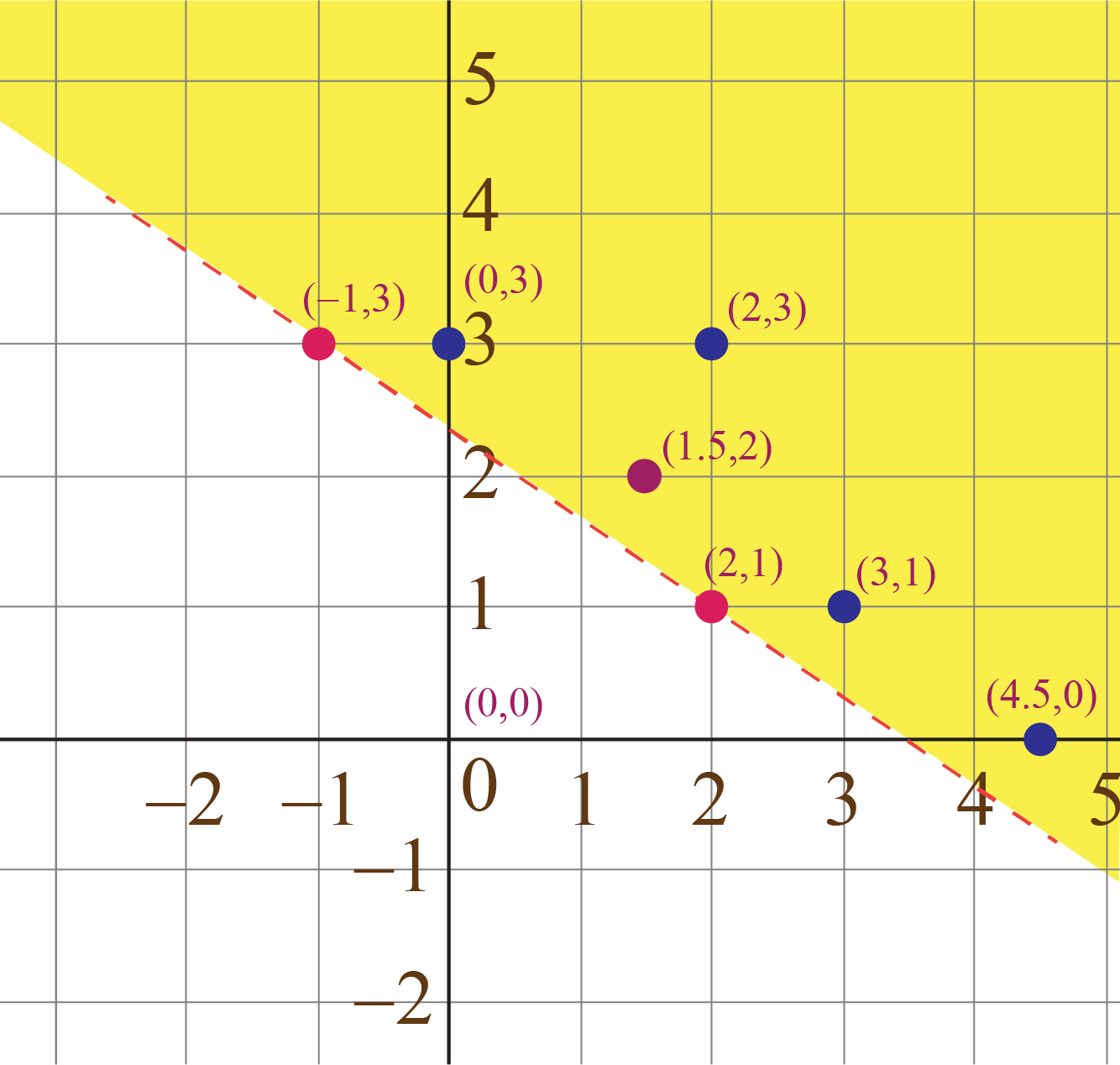
All the five points (corresponding to the five solutions) lie above the line . 

• Take any point which lies above the line. Its coordinates, say \(\left( {{x_0},\;{y_0}} \right),\), will satisfy the inequality: \[2{x_0} + 3{y_0} >7\]
• This means that the solution set for the inequality consists of all points lying above the line .
• Put x = 0, y = 0, which gives 2(0) + 3(0) > 7, which further gives 0 > 7.This doesn't holds true for the given inequality. So, shade the half plane which doesn't include the point (0,0).

• Inequalities can be solved by adding, subtracting, multiplying, or dividing both sides by the same number.
• Dividing or multiplying both sides by negative numbers will alter the inequality's direction.
• Ordered pairs outside the shaded region don't solve linear inequalities.
• Less and greater than are strict inequalities while less than or equal to and greater than or equal to are not strict inequalities.
• Any line will divide the plane in which it lies into two half-planes.
• The solution sets of linear inequalities correspond to half-planes, while the solution sets of linear equations corresponds to lines.

Solved Examples 

Help Bob to determine if (2,1/5) is a solution to \[2x + 5y < 10\]

Let's put these values (2,1/5) in the given linear inequality.

This gives \begin{equation} 2(2)+5(1 / 5)<10 \end{equation}

 \begin{equation}4 + 1 < 10\end{equation}

 \begin{equation}5 < 10\end{equation} which holds true.

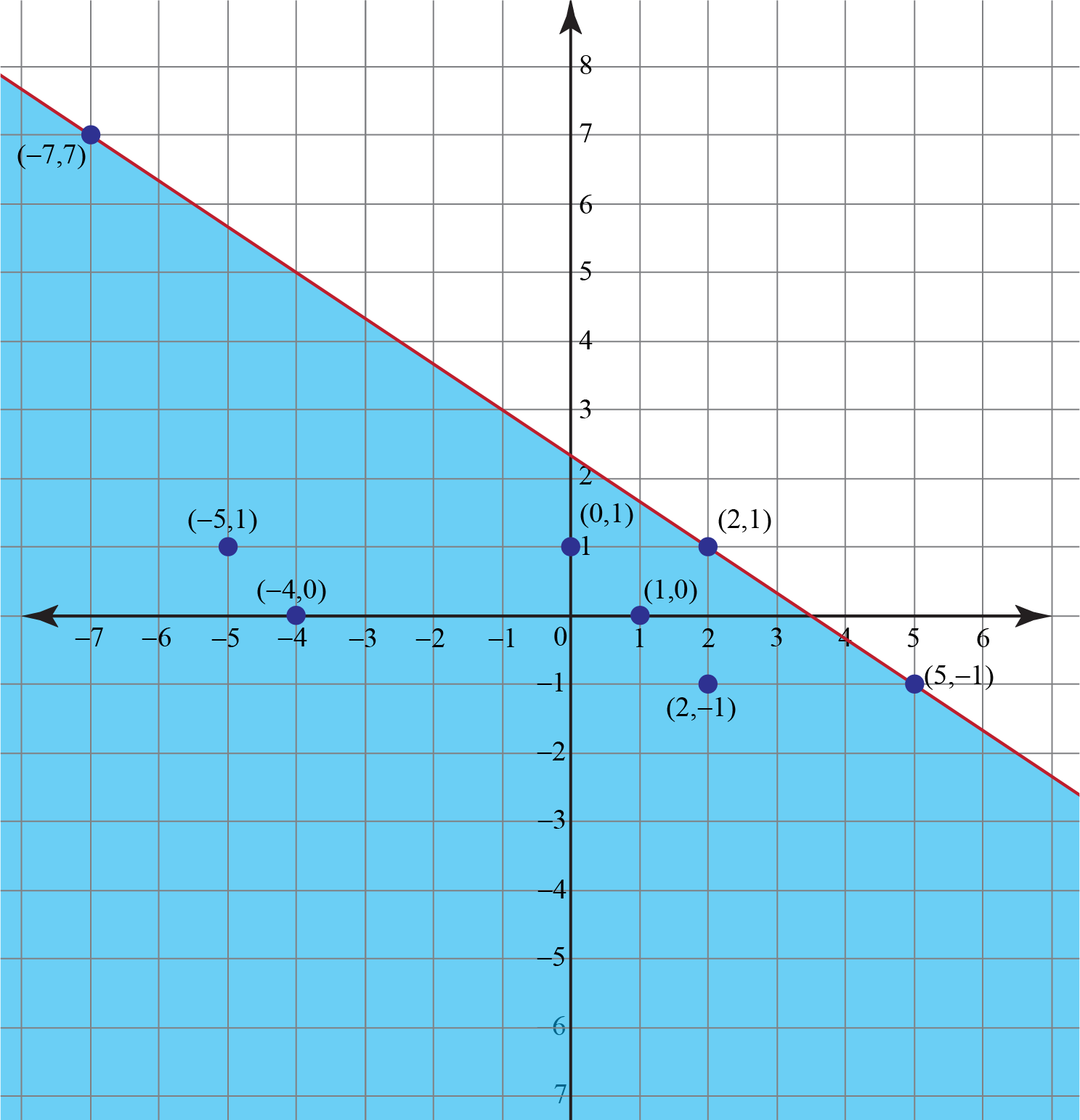
Brook's mother hands over $7 to him for chocolates. She tells him to spend only $7 or less than that. 

A milk chocolate costs $2 while a nuts chocolate costs $33.

Let x be the number of milk chocolates and y be the number of nuts chocolates.

Form an inequality corresponding to the above situation and graph the inequality.

\[2x + 3y ≤ 7\] will be the inequality corresponding to the above situation.

In this case, we will plot a solid line as boundary joining the points which satisfy the linear equation \[2x + 3y=7\]

For \[2x + 3y=7\]

For inequality \[2x + 3y ≤ 7\]

• Determine some specific solutions for the linear inequality  \[2x + 3y ≤ 7\] which can be as follows: \begin{equation}(0,1),(-4,0),(1,0),(-5,1),(2,-1)\end{equation}
• Plot these points. These will lie below the solid line. 

Now, put x = 0, y = 0

This gives, 2(0) + 3(0) ≤  7, which satisfies the inequality.

So, shade the half plane in the linear inequality graph below, which includes the point (0,0).

Graph the solution set for \[y > -5x + 2 \]

\[y > -5x + 2 \] is an inequality in slope intercept form; slope=-5, intercept=2.

In this case, we will plot a dashed line because of a less than or equal to equality, as boundary joining the points which satisfy the linear equation  \[y = -5x + 2\]

For \[y = -5x + 2\]

For the inequality\[y > -5x + 2 \]

• Determine some specific solutions for the linear inequality \[y > -5x + 2 \] which can be as follows: \begin{equation}(1,2), (3,-2), (4,3), (4,5), (3,6)\end{equation}
• Plot these points. These will lie above the dotted line.

For \[y > -5x + 2 \] put x=0, y=0

This gives 0>-5(0)+2

which further gives 0>2

This doesn't hold true for the given inequality. So, shade the half plane in the linear inequality graph below, which doesn't includes the point (0,0).

Interactive Questions

Here are a few activities for you to practice.

Select/Type your answer and click the "Check Answer" button to see the result.

Let's Summarize

We hope you enjoyed learning about what are linear inequalities with two variables, solving linear inequalities with two variables, graphing two variable inequalities, infinite sets, ordered pairs, greater than or equal to &, less than or equal to with interactive questions. Now, you will be able to easily find answers to linear inequalities with two variables and knowing about linear inequalities solutions.

The mini-lesson targeted the fascinating concept of linear inequalities in two variables. The math journey around linear inequalities in two variables starts with what a student already knows, and goes on to creatively crafting a fresh concept in the young minds. Done in a way that is not only relatable and easy to grasp, but will also stay with them forever. Here lies the magic with Cuemath.

About Cuemath

At  Cuemath , our team of math experts is dedicated to making learning fun for our favorite readers, the students!

Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.

Be it worksheets, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we at Cuemath believe in.

FAQs o n  L inear Inequalities in Two Variables

1. what is a system of linear inequalities in two variables.

A system of linear inequalities in two variables refers to a set at least two linear inequalities in the same variables.

2. How do you differentiate linear inequalities in two variables from linear equations in two variables?

The graph of linear equations include a solid line in every situation, whereasin case of linear inequalities, the graph includes either a dashed line or a solid line. Also, linear inequalities include shaded regions but linear equations do not.

3. What is an example of a linear inequality?

An example Linear Inequality can be any linear equation but with symbols like <, >, ≤, or ≥ instead of an =.

4. What are the symbols used in linear inequalities?

The symbols used in linear inequalities are <, ≤, >, and ≥.

5. What is the meaning of linear inequalities?

A linear inequality is an inequality having a linear function, consisting of one of the symbols of inequality.

6. How do you identify a linear inequality?

When the two sides of an equation have sign other than equal to.

7. What is the use of linear inequalities?

A system of linear inequalities is often used to determine the maximum or minimum values of a situation with multiple constraints.

8. What are the 5 inequality symbols?

The five inequality symbols are ≠ = not equal to, > = greater than, < = less than, ≥ = greater than or equal to & ≤ = less than or equal to.

9. What does R mean in inequalities?

In inequalities, R corresponds to real numbers and includes all real numbers.

• For educators
• English (US)
• English (India)
• English (UK)
• Greek Alphabet

This problem has been solved!

You'll get a detailed solution from a subject matter expert that helps you learn core concepts.

Question: Assignment 6.1: Solution of Linear Inequalities by Graphical Method Start Assign Due No Due Date Points 30 Submitting a file upload Available Apr 27 at 1:40pm - Apr 28 at 5:30pm 1 day Attempts 0 Allowed Attempts 1 1. Directions: Upload your answer here. 10 pts, each number II. Use graphing paper to graph the solution set of the following system of linear

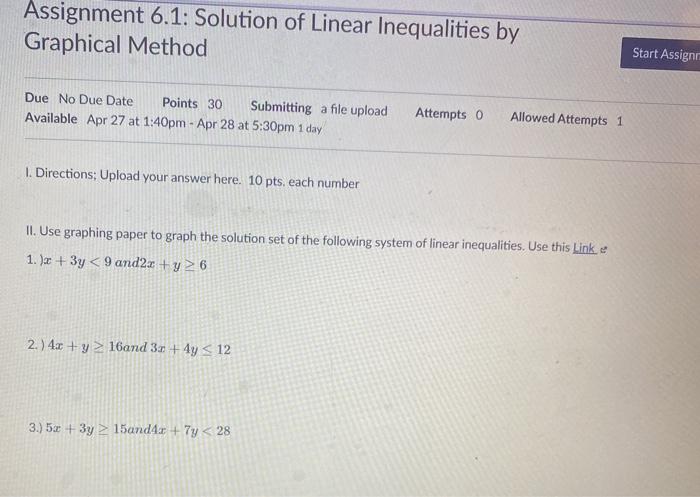
This AI-generated tip is based on Chegg's full solution. Sign up to see more!

Identify the boundary lines for the inequalities by converting each inequality to its equivalent equation by using the "=" sign instead of "<" or "≥".

1) Graph Red : x+3y < 9 B …

Not the question you’re looking for?

Post any question and get expert help quickly.

Module 2: Linear Inequalities and Absolute Values

2.1: linear inequalities with one variable, section 2.1 learning objectives.

2.1:  Linear Inequalities with One Variable

• Express solutions to inequalities graphically, with interval notation, and with set-builder notation
• Solve single-step linear inequalities with one variable
• Combine properties of inequality to solve linear inequalities with one variable
• Simplify using the Distributive Property and solve linear inequalities with one variable

Writing inequalities

First, let’s define some important terminology. An inequality is a mathematical statement that compares two expressions using the ideas of greater than or less than. Special symbols are used in these statements. When you read an inequality, read it from left to right—just like reading text on a page. In algebra, inequalities are used to describe large sets of solutions. Sometimes there are an infinite amount of numbers that will satisfy an inequality, so rather than try to list off an infinite amount of numbers, we have developed some ways to describe very large lists in succinct ways.

The first way you are probably familiar with—the basic inequality. For example:

• [latex]{x}\lt{9}[/latex] indicates the list of numbers that are less than 9. Would you rather write [latex]{x}\lt{9}[/latex] or try to list all the possible numbers that are less than 9? (hopefully, your answer is “no”, you don’t want to try to list them all.)
• [latex]-5\le{t}[/latex] indicates all the numbers that are greater than or equal to [latex]-5[/latex].

Note how placing the variable on the left or right of the inequality sign can change whether you are looking for greater than or less than.

For example:

• [latex]x\lt5[/latex] means all the real numbers that are less than 5, whereas;
• [latex]5\lt{x}[/latex] means that 5 is less than x, or we could rewrite this with the x on the left: [latex]x\gt{5}[/latex]. Note how the inequality is still pointing the same direction relative to x. This statement represents all the real numbers that are greater than 5, which is easier to interpret than 5 is less than x.

The second way is with a graph using the number line:

The third way is with an interval.

The fourth way is using set-builder notation.

We will explore the second, third, and fourth ways in depth in this section. Again, those four ways to write solutions to inequalities are:

• an inequality
• an interval
• using set-builder notation

Inequality Signs

The box below shows the symbol, meaning, and an example for each inequality sign. Sometimes it’s easy to get tangled up in inequalities, just remember to read them from left to right.

The inequality [latex]x>y[/latex] can also be written as [latex]{y}<{x}[/latex]. The sides of any inequality can be switched as long as the inequality symbol between them is also reversed.

Graphing an inequality

Inequalities can also be graphed on a number line. Below are three examples of inequalities and their graphs.  Graphs are a very helpful way to visualize information – especially when that information represents an infinite list of numbers!

[latex]x\leq -4[/latex]. This translates to all the real numbers on a number line that are less than or equal to -4.

[latex]{x}\geq{-3}[/latex]. This translates to all the real numbers on the number line that are greater than or equal to -3.

Each of these graphs begins with a circle—either an open or closed (shaded) circle. This point is often called the end point of the solution. A closed, or shaded, circle is used to represent the inequalities greater than or equal to  [latex] \displaystyle \left(\geq\right) [/latex] or less than or equal to  [latex] \displaystyle \left(\leq\right) [/latex]. The point is part of the solution. An open circle is used for greater than (>) or less than (<). The point is not part of the solution.

The graph then extends endlessly in one direction. This is shown by a line with an arrow at the end. For example, notice that for the graph of [latex] \displaystyle x\geq -3[/latex] shown above, the end point is [latex]−3[/latex], represented with a closed circle since the inequality is greater than or equal to [latex]−3[/latex]. The blue line is drawn to the right on the number line because the values in this area are greater than [latex]−3[/latex]. The arrow at the end indicates that the solutions continue infinitely.

Graph the inequality [latex]x\ge 4[/latex].

We can use a number line as shown. Because the values for x include 4, we place a solid dot on the number line at 4.

Then we draw a line that begins at [latex]x=4[/latex] and, as indicated by the arrowhead, continues to positive infinity, which illustrates that the solution set includes all real numbers greater than or equal to 4.

Write an inequality describing all the real numbers on the number line that are less than 2, then draw the corresponding graph.

We need to start from the left and work right, so we start from negative infinity and end at [latex]-2[/latex]. We will not include either because infinity is not a number, and the inequality does not include [latex]-2[/latex].

Inequality: [latex]x<2[/latex]

To draw the graph, place an open dot on the number line first, then draw a line extending to the left. Draw an arrow at the leftmost point of the line to indicate that it continues for infinity.

Represent inequalities using interval notation

Another commonly used, and arguably the most concise, method for describing inequalities and solutions to inequalities is called  interval notation.  With this convention, sets are built with parentheses or brackets, each having a distinct meaning. The solutions to [latex]x\geq 4[/latex] are represented as [latex]\left[4,\infty \right)[/latex]. This method is widely used and will be present in other math courses you may take.

The main concept to remember is that parentheses represent solutions greater or less than the number, and brackets represent solutions that are greater than or equal to or less than or equal to the number. Use parentheses to represent infinity or negative infinity, since positive and negative infinity are not numbers in the usual sense of the word and, therefore, cannot be “equaled.” A few examples of an interval , or a set of numbers in which a solution falls, are [latex]\left[-2,6\right)[/latex], or all numbers between [latex]-2[/latex] and [latex]6[/latex], including [latex]-2[/latex], but not including [latex]6[/latex]; [latex]\left(-1,0\right)[/latex], all real numbers between, but not including [latex]-1[/latex] and [latex]0[/latex]; and [latex]\left(-\infty,1\right][/latex], all real numbers less than and including [latex]1[/latex]. To construct intervals, start with the value that is furthest left on the number line as the left value, such as [latex]\left[-2,6\right)[/latex], where -2 is less than 6. The number on the right should be greater than the number on the left. While not technically numbers, this ordering extends to positive and negative infinity as well.

The table below describes all the possible inequalities that can occur and how to write them using interval notation, where a and b are real numbers.  Remember to read inequalities from left to right, just like text.

Describe the inequality [latex]x\ge 4[/latex] using interval notation.

The solutions to [latex]x\ge 4[/latex] are represented as [latex]\left[4,\infty \right)[/latex].

Note the use of a bracket on the left because 4 is included in the solution set.

Use interval notation to indicate all real numbers less than or equal to [latex]-2[/latex].

Use a parentheses on the left of [latex]-\infty[/latex] and bracket after [latex]-2[/latex]: [latex]\left(-\infty,-2 \right][/latex]. The bracket indicates that [latex]-2[/latex] is included in the set with all real numbers less than or equal to -2, which includes all real numbers from negative infinity to [latex]-2[/latex].

Think About It 1

In the previous examples you were given an inequality or a description of one with words and asked to draw the corresponding graph and write the interval. In this example you are given an interval and asked to write the inequality and draw the graph.

Given [latex]\left(-\infty,10\right)[/latex], write the associated inequality and draw the graph.

In the box below, write down whether you think it will be easier to draw the graph first or write the inequality first.

We will draw the graph first.

The interval reads “all real numbers less than 10,” so we will start by placing an open dot on 10 and drawing a line to the left with an arrow indicating the solution continues to negative infinity.

To write the inequality, we will use < since the parentheses indicate that 10 is not included. [latex]x<10[/latex]

In the following video, you will see examples of how to draw a graph given an inequality in interval notation.

And finally, one last video that shows how to write inequalities using a graph, with interval notation and as an inequality.

Represent inequalities using set-builder notation

Another method used for describing inequalities and solutions to inequalities is called set-builder notation.  In this method, we show the conditions a variable must meet in order to be part of a set.

If we want to describe the set of all Real numbers that are greater than 0 using set-builder notation, it would look like the following:

[latex]{\color{red}\{}{\color{green}x}\hspace{.01in}{\mathbf{\color{blue}|}}\hspace{.01in}x>0{\color{red}\}}[/latex]

The parentheses indicate that we have a set. The vertical line, |, is read “such that”. Therefore, the example above would read as:

“ The set of all x such that  x is greater than 0.”

Let’s look at one more example.  Let’s use set-builder notation to describe the set of all Real numbers that are between 4 and 10, including 10.

[latex]{\color{red}\{}{\color{green}x}\hspace{.01in}{\mathbf{\color{blue}|}}\hspace{.01in}4<x\le10{\color{red}\}}[/latex]

The set of all x such that  x is between 4 and 10, including 10.

Describe the inequality [latex]1≤x<8[/latex] using set-builder notation.

[latex]\{{x|1≤x<8}\}[/latex]

Use set-builder notation to indicate all Real numbers less than -6 .

[latex]\{{x|x<-6}\}[/latex]

This describes the set of all Real numbers less than -6.

Solving single-step inequalities

Solve inequalities with addition and subtraction.

You can solve most inequalities using inverse operations  as you did for solving equations.  This is because when you add or subtract the same value from both sides of an inequality, you have maintained the inequality. These properties are outlined in the box below.

Addition and Subtraction Properties of Inequality

If [latex]a>b[/latex],   then [latex]a+c>b+c[/latex].

If [latex]a>b[/latex] , then [latex]a−c>b−c[/latex].

Because inequalities have multiple possible solutions, representing the solutions graphically provides a helpful visual of the situation, as we saw in the last section. The example below shows the steps to solve and graph an inequality and express the solution using interval notation.

Solve for x.

[latex] {x}+3\lt{5}[/latex]

It is helpful to think of this inequality as asking you to find all the values for x , including negative numbers, such that when you add three you will get a number less than 5.

[latex] \displaystyle \begin{array}{l}x+3<\,\,\,\,5\\\underline{\,\,\,\,\,-3\,\,\,\,-3}\\x\,\,\,\,\,\,\,\,<\,\,\,\,2\,\,\end{array}[/latex]

Isolate the variable by subtracting 3 from both sides of the inequality.

Inequality:  [latex]x<2[/latex]

Interval:  [latex]\left(-\infty, 2\right)[/latex]

The line represents all the numbers to which you can add 3 and get a number that is less than 5. There’s a lot of numbers that solve this inequality!

Just as you can check the solution to an equation, you can check a solution to an inequality. First, you check the end point by substituting it in the related equation. Then you check to see if the inequality is correct by substituting any other solution to see if it is one of the solutions. Because there are multiple solutions, it is a good practice to check more than one of the possible solutions. This can also help you check that your graph is correct.

The example below shows how you could check that [latex]x<2[/latex]   is the solution to [latex]x+3<5[/latex] .

Check that [latex]x<2[/latex]   is the solution to [latex]x+3<5[/latex].

Substitute the end point 2 into the related equation, [latex]x+3=5[/latex].

[latex]\begin{array}{r}x+3=5 \\ 2+3=5 \\ 5=5\end{array}[/latex]

Pick a value less than 2, such as 0, to check into the inequality. (This value will be on the shaded part of the graph.)

[latex] \displaystyle \begin{array}{r}x+3<5 \\ 0+3<5 \\ 3<5\end{array}[/latex]

[latex]x<2[/latex] is the solution to [latex]x+3<5[/latex].

The following examples show inequality problems that include operations with negative numbers. The graph of the solution to the inequality is also shown. Remember to check the solution. This is a good habit to build!

Solve for x : [latex]\hspace{.05in}x-10\leq-12[/latex]

Isolate the variable by adding 10 to both sides of the inequality.

[latex] \displaystyle \begin{array}{r}x-10\le -12\\\underline{\,\,\,+10\,\,\,\,\,+10}\\x\,\,\,\,\,\,\,\,\,\,\le \,\,\,-2\end{array}[/latex]

Check the solution to [latex]x-10\leq -12[/latex]

Substitute the end point [latex]−2[/latex] into the related equation  [latex]x-10=−12[/latex]

[latex] \displaystyle \begin{array}{r}x-10=-12\,\,\,\\\text{Does}\,\,\,-2-10=-12?\\-12=-12\,\,\,\end{array}[/latex]

Pick a value less than [latex]−2[/latex], such as [latex]−5[/latex], to check in the inequality. (This value will be on the shaded part of the graph.)

[latex] \displaystyle \begin{array}{r}x-10\le -12\,\,\,\\\text{ }\,\text{ Is}\,\,-5-10\le -12?\\-15\le -12\,\,\,\\\text{It}\,\text{checks!}\end{array}[/latex]

[latex]x\leq -2[/latex] is the solution to [latex]x-10\leq -12[/latex]

Solve for a : [latex]\hspace{.05in}a-17>-17[/latex]

Isolate the variable by adding 17 to both sides of the inequality.

[latex] \displaystyle \begin{array}{r}a-17>-17\\\underline{\,\,\,+17\,\,\,\,\,+17}\\a\,\,\,\,\,\,\,\,\,\,\,>\,\,\,\,\,\,0\end{array}[/latex]

Inequality: [latex] \displaystyle a\,\,>\,0[/latex]

Interval: [latex]\left(0,\infty\right)[/latex]  Note how we use parentheses on the left to show that the solution does not include 0.

Graph: Note the open circle to show that the solution does not include 0.

Check the solution to [latex]a-17>-17[/latex]

Is [latex] \displaystyle a\,\,>\,0[/latex] the correct solution to  [latex]a-17>-17[/latex]?

Substitute the end point 0 into the related equation.

[latex] \displaystyle \begin{array}{r}a-17=-17\,\,\,\\\text{Does}\,\,\,0-17=-17?\\-17=-17\,\,\,\end{array}[/latex]

Pick a value greater than 0, such as 20, to check in the inequality. (This value will be on the shaded part of the graph.)

[latex] \displaystyle \begin{array}{r}a-17>-17\,\,\,\\\text{Is }\,\,20-17>-17?\\3>-17\,\,\,\\\\\text{It checks!}\,\,\,\,\end{array}[/latex]

[latex] \displaystyle a\,>\,0[/latex] is the solution to [latex]a-17>-17[/latex]

The previous examples showed you how to solve a one-step inequality with the variable on the left hand side.  The following video provides examples of how to solve the same type of inequality.

What would you do if the variable were on the right side of the inequality?  In the following example, you will see how to handle this scenario.

Solve for x : [latex]\hspace{.05in}4\geq{x}+5[/latex]

Isolate the variable by subtracting 5 from both sides of the inequality.

[latex] \displaystyle \begin{array}{r}4\geq{x}+5 \\\underline{\,\,\,-5\,\,\,\,\,-5}\\-1\,\,\,\,\,\,\,\,\,\,\ge \,\,\,x\end{array}[/latex]

Rewrite the inequality with the variable on the left – this makes writing the interval and drawing the graph easier.

[latex]x\le{-1}[/latex]

Note how the the pointy part of the inequality is still directed at the variable, so instead of reading as negative one is greater or equal to x, it now reads as x is less than or equal to negative one.

Check the solution to [latex]4\geq{x}+5[/latex]

Substitute the end point [latex]−1[/latex] into the related equation  [latex]4=x+5[/latex]

[latex] \displaystyle \begin{array}{r}4=x+5\,\,\,\\\text{Does}\,\,\,4=-1+5?\\-1=-1\,\,\,\end{array}[/latex]

Pick a value less than [latex]−1[/latex], such as [latex]−5[/latex], to check in the inequality. (This value will be on the shaded part of the graph.)

[latex] \displaystyle \begin{array}{r}4\geq{-5}+5\,\,\,\\\text{ }\,\text{ Is}\,\,4\ge 0?\\\text{It}\,\text{checks!}\end{array}[/latex]

Solve inequalities with multiplication and division

Solving an inequality with a variable that has a coefficient other than 1 usually involves multiplication or division. The steps are like solving one-step equations involving multiplication or division EXCEPT for the inequality sign. Let’s look at what happens to the inequality when you multiply or divide each side by the same number.

Multiplication and Division Properties of Inequality

Keep in mind that you only change the sign when you are multiplying and dividing by a negative number. If you add or subtract by a negative number, the inequality stays the same.

Solve for x:  [latex]\hspace{.05in}3x>12[/latex]

[latex] \displaystyle \begin{array}{r}\underline{3x}>\underline{12}\\3\,\,\,\,\,\,\,\,\,\,\,\,3\\x>4\,\,\,\end{array}[/latex]

Check your solution by first checking the end point 4, and then checking another solution for the inequality.

[latex]\begin{array}{r}3\cdot4=12\\12=12\\3\cdot10>12\\30>12\\\text{It checks!}\end{array}[/latex]

Inequality: [latex] \displaystyle x>4[/latex]

Interval: [latex]\left(4,\infty\right)[/latex]

There was no need to make any changes to the inequality sign because both sides of the inequality were divided by positive 3. In the next example, there is division by a negative number, so there is an additional step in the solution!

Solve for x : [latex]\hspace{.05in}−2x>6[/latex]

[latex] \displaystyle \begin{array}{r}\underline{-2x}>\underline{\,6\,}\\-2\,\,\,\,-2\,\\x<-3\end{array}[/latex]

Check your solution by first checking the end point [latex]−3[/latex], and then checking another solution for the inequality.

[latex]\begin{array}{r}-2\left(-3\right)=6 \\6=6\\ -2\left(-6\right)>6 \\ 12>6\end{array}[/latex]

Inequality: [latex] \displaystyle x<-3[/latex]

Interval: [latex]\left(-\infty, -3\right)[/latex]

The following video shows examples of solving one step inequalities using the Multiplication Property of Equality where the variable is on the left hand side.

Think About It 2

Before you read the solution to the next example, think about what properties of inequalities you may need to use to solve the inequality. What is different about this example from the previous one? Write your ideas in the box below.

Solve for x : [latex]\hspace{.05in}-\frac{1}{2}>-12x[/latex]

This inequality has the variable on the right hand side, which is different from the previous examples. Start the solution process as before, and at the end, you can move the variable to the left to write the final solution.

Divide both sides by [latex]-12[/latex] to isolate the variable. Since you are dividing by a negative number, you will need to change the direction of the inequality sign.

[latex]\displaystyle\begin{array}{l}-\frac{1}{2}\gt{-12x}\\\\\frac{-\frac{1}{2}}{-12}\gt\frac{-12x}{-12}\\\end{array}[/latex]

Notice the change of direction of the inequality sign below. Also, dividing a fraction by an integer requires you to multiply by the reciprocal, and the reciprocal of [latex]-12[/latex] is [latex]\frac{1}{-12}[/latex]

[latex]\displaystyle\begin{array}{r}\left(-\frac{1}{12}\right)\left(-\frac{1}{2}\right)\lt\frac{-12x}{-12}\,\,\\\\ \frac{1}{24}\lt\frac{\cancel{-12}x}{\cancel{-12}}\\\\ \frac{1}{24}\lt{x}\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

Inequality: [latex]\frac{1}{24}\lt{x}[/latex]  This can also be written with the variable on the left as [latex]x\gt\frac{1}{24}[/latex].  Writing the inequality with the variable on the left requires a little thinking, but helps you write the interval and draw the graph correctly.

Interval: [latex]\left(\frac{1}{24},\infty\right)[/latex]

The following video gives examples of how to solve an inequality with the Multiplication Property of Equality where the variable is on the right hand side.

Combining properties of inequality to solve algebraic inequalities

A popular strategy for solving equations, isolating the variable, also applies to solving inequalities. By adding, subtracting, multiplying and/or dividing, you can rewrite the inequality so that the variable is on one side and everything else is on the other. As with one-step inequalities, the solutions to multi-step inequalities can be graphed on a number line.

Solve for p : [latex]\hspace{.05in}4p+5<29[/latex]

Begin to isolate the variable by subtracting 5 from both sides of the inequality.

[latex] \displaystyle \begin{array}{l}4p+5<\,\,\,29\\\underline{\,\,\,\,\,\,\,\,\,-5\,\,\,\,\,-5}\\4p\,\,\,\,\,\,\,\,\,<\,\,24\,\,\end{array}[/latex]

Divide both sides of the inequality by 4 to express the variable with a coefficient of 1.

[latex]\begin{array}{l}\underline{4p}\,<\,\,\underline{24}\,\,\\\,4\,\,\,\,<\,\,4\\\,\,\,\,\,p<6\end{array}[/latex]

Inequality: [latex]p<6[/latex]

Interval: [latex]\left(-\infty,6\right)[/latex]

Graph: Note the open circle at the end point 6 to show that solutions to the inequality do not include 6. The values where p is less than 6 are found all along the number line to the left of 6.

Check the solution.

Check the end point 6 in the related equation.

[latex] \displaystyle \begin{array}{r}4p+5=29\,\,\,\\\text{Does}\,\,\,4(6)+5=29?\\24+5=29\,\,\,\\29=29\,\,\,\\\text{Yes!}\,\,\,\,\,\,\end{array}[/latex]

Try another value to check the inequality. Let’s use [latex]p=0[/latex].

[latex] \displaystyle \begin{array}{r}4p+5<29\,\,\,\\\text{Is}\,\,\,4(0)+5<29?\\0+5<29\,\,\,\\5<29\,\,\,\\\text{Yes!}\,\,\,\,\,\end{array}[/latex]

[latex]p<6[/latex] is the solution to [latex]4p+5<29[/latex]

Solve for x :  [latex]\hspace{.05in}3x–7\ge 41[/latex]

Begin to isolate the variable by adding 7 to both sides of the inequality, then divide both sides of the inequality by 3 to express the variable with a coefficient of 1.

[latex] \displaystyle \begin{array}{l}3x-7\ge 41\\\underline{\,\,\,\,\,\,\,+7\,\,\,\,+7}\\\frac{3x}{3}\,\,\,\,\,\,\,\,\ge \frac{48}{3}\\\,\,\,\,\,\,\,\,\,\,x\ge 16\end{array}[/latex]

Inequality: [latex]x\ge 16[/latex]

Interval: [latex]\left[16,\infty\right)[/latex]

First, check the end point 16 in the related equation.

[latex] \displaystyle \begin{array}{r}3x-7=41\,\,\,\\\text{Does}\,\,\,3(16)-7=41?\\48-7=41\,\,\,\\41=41\,\,\,\\\text{Yes!}\,\,\,\,\,\end{array}[/latex]

Then, try another value to check the inequality. Let’s use [latex]x = 20[/latex].

[latex] \displaystyle \begin{array}{r}\,\,\,\,3x-7\ge 41\,\,\,\\\text{Is}\,\,\,\,\,3(20)-7\ge 41?\\60-7\ge 41\,\,\,\\53\ge 41\,\,\,\\\text{Yes!}\,\,\,\,\,\end{array}[/latex]

When solving multi-step equations, pay attention to situations in which you multiply or divide by a negative number. In these cases, you must reverse the inequality sign.

Solve for p : [latex]\hspace{.05in}−58>14−6p[/latex]

Note how the variable is on the right hand side of the inequality, the method for solving does not change in this case.

Begin to isolate the variable by subtracting 14 from both sides of the inequality.

[latex] \displaystyle \begin{array}{l}−58\,\,>14−6p\\\underline{-14\,\,\,-14}\\-72\,\,>-6p\end{array}[/latex]

Divide both sides of the inequality by [latex]−6[/latex] to express the variable with a coefficient of 1. Dividing by a negative number results in reversing the inequality sign.

[latex]\begin{array}{l}\underline{-72}>\underline{-6p}\\-6\,\,\,\,\,\,\,\,\,\,-6\\\,\,\,\,\,\,12\lt{p}\end{array}[/latex]

We can also write this as [latex]p>12[/latex].   Notice how the inequality sign is still opening up toward the variable p.

Inequality: [latex]p>12[/latex] Interval: [latex]\left(12,\infty\right)[/latex] Graph: The graph of the inequality p > 12 has an open circle at 12 with an arrow stretching to the right.

First, check the end point 12 in the related equation.

[latex]\begin{array}{r}-58=14-6p\\-58=14-6\left(12\right)\\-58=14-72\\-58=-58\end{array}[/latex]

Then, try another value to check the inequality. Try 100.

[latex]\begin{array}{r}-58>14-6p\\-58>14-6\left(100\right)\\-58>14-600\\-58>-586\end{array}[/latex]

In the following video, you will see an example of solving a linear inequality with the variable on the left side of the inequality, and an example of switching the direction of the inequality after dividing by a negative number.

In the following video, you will see an example of solving a linear inequality with the variable on the right side of the inequality, and an example of switching the direction of the inequality after dividing by a negative number.

Simplifying and solving algebraic inequalities using the Distributive Property

As with equations, the Distributive Property can be applied to simplify expressions that are part of an inequality. Once the parentheses have been cleared, solving the inequality will be straightforward.

Solve for x:  [latex]\hspace{.05in}2\left(3x–5\right)\leq 4x+6[/latex]

Distribute to clear the parentheses.

[latex] \displaystyle \begin{array}{r}\,2(3x-5)\leq 4x+6\\\,\,\,\,6x-10\leq 4x+6\end{array}[/latex]

Subtract 4 x from both sides to get the variable term on one side only.

[latex]\begin{array}{r}6x-10\le 4x+6\\\underline{-4x\,\,\,\,\,\,\,\,\,\,\,\,\,\,-4x}\,\,\,\,\,\,\,\,\,\\\,\,\,2x-10\,\,\leq \,\,\,\,\,\,\,\,\,\,\,\,6\end{array}[/latex]

Add 10 to both sides to isolate the variable.

[latex]\begin{array}{r}\\\,\,\,2x-10\,\,\le \,\,\,\,\,\,\,\,6\,\,\,\\\underline{\,\,\,\,\,\,+10\,\,\,\,\,\,\,\,\,+10}\\\,\,\,2x\,\,\,\,\,\,\,\,\,\,\,\le \,\,\,\,\,16\,\,\,\end{array}[/latex]

Divide both sides by 2 to express the variable with a coefficient of 1.

[latex]\begin{array}{r}\underline{2x}\le \,\,\,\underline{16}\\\,\,\,2\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\le \,\,\,\,\,8\end{array}[/latex]

Inequality: [latex]x\le8[/latex] Interval: [latex]\left(-\infty,8\right][/latex] Graph: The graph of this solution set includes 8 and everything left of 8 on the number line.

First, check the end point 8 in the related equation.

[latex] \displaystyle \begin{array}{r}2(3x-5)=4x+6\,\,\,\,\,\,\\2(3\,\cdot \,8-5)=4\,\cdot \,8+6\\\,\,\,\,\,\,\,\,\,\,\,2(24-5)=32+6\,\,\,\,\,\,\\2(19)=38\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\38=38\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

Then, choose another solution and evaluate the inequality for that value to make sure it is a true statement. Try 0.

[latex] \displaystyle \begin{array}{l}2(3\,\cdot \,0-5)\le 4\,\cdot \,0+6?\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2(-5)\le 6\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-10\le 6\,\,\end{array}[/latex]

[latex]x\le8[/latex] is the solution to [latex]\left(-\infty,8\right][/latex]

Think About It 3

In the next example, you are given an inequality with a term that looks complicated. If you pause and think about how to use the order of operations to solve the inequality, it will hopefully seem like a straightforward problem. Use the textbox to write down what you think is the best first step to take.

Solve for a: [latex]\hspace{.05in}\displaystyle\frac{{2}{a}-{4}}{{-6}}{>-2}[/latex]

Clear the fraction by multiplying both sides of the equation by [latex]-6[/latex].  While we encounter division much more often in the solving process, do not forget that multiplying by a negative number will also require us to reverse the inequality symbol.

[latex]\displaystyle \begin{array}{r}\frac{{2}{a}-{4}}{{-6}}{>-2}\,\,\,\,\,\,\,\,\\\\-6\,\cdot \,\frac{2a-4}{-6}<-2\,\cdot \,-6\\\\{2a-4}<12\,\,\,\,\,\,\end{array}[/latex]

Add 4 to both sides to isolate the variable.

[latex]\displaystyle \begin{array}{r}2a-4<12\\\underline{\,\,\,+4\,\,\,\,+4}\\2a<16\end{array}[/latex]

[latex] \displaystyle \begin{array}{c}\frac{2a}{2}<\,\frac{16}{2}\\\\a<8\end{array}[/latex]

Inequality: [latex]a<8[/latex]

Interval: [latex]\left(-\infty,8\right)[/latex]

[latex] \displaystyle \begin{array}{r}\frac{2a-4}{-6}=-2\,\,\,\,\\\\\text{Does}\,\,\,\frac{2(8)-4}{-6}=-2?\\\\\frac{16-4}{-6}=-2\,\,\,\,\\\\\frac{12}{-6}=-2\,\,\,\,\\\\-2=-2\,\,\,\,\\\\\text{Yes!}\,\,\,\,\,\end{array}[/latex]

Then choose another solution and evaluate the inequality for that value to make sure it is a true statement. Try 5.

[latex] \displaystyle \begin{array}{r}\text{Is}\,\,\,\frac{2(5)-4}{-6}>-2?\\\\\frac{10-4}{-6}>-2\,\,\,\\\\\,\,\,\,\frac{6}{-6}>-2\,\,\,\\\\-1>-2\,\,\,\\\\\text{Yes!}\,\,\,\,\,\end{array}[/latex]

Solving inequalities is very similar to solving equations, except you have to reverse the inequality symbols when you multiply or divide both sides of an inequality by a negative number. There are four ways to represent solutions to inequalities: an inequality, a graph, an interval, and using set-builder notation. Because there is usually more than one solution to an inequality, when you check your answer you should check the end point and one other value to check the direction of the inequality.

Inequalities can have a range of answers. The solutions are often graphed on a number line in order to visualize all of the solutions. Multi-step inequalities are solved using the same processes that work for solving equations with one exception. When you multiply or divide both sides of an inequality by a negative number, you must reverse the inequality symbol. The inequality symbols stay the same whenever you add or subtract either positive or negative numbers to both sides of the inequality.